发布日期: 2023-04-15

作者: xhsioi

文章字数: 7.2k

阅读时长: 30 分

阅读次数:

华为软件精英挑战赛——普朗克计划

2023华为软件精英挑战赛——普朗克计划

2023/3/26

https://competition.huaweicloud.com/codecraft2023

云智能机器人协同调度优化

背景信息

机器人已经在智能制造、物流仓储、递送、医疗等很多领域显现出巨大的市场需求与商业价值。在机器人领域，华为云聚焦于探索云计算如何给当前机器人产业带来增量价值，包括：极速开发、敏捷交付、以云助端、数据驱动、终身学习、高效运维。通过对机器人建图、仿真、技能开发、运行管理等方向云原生化，已验证云可为机器人递送、巡检等场景带来TTM和成本 80%的降低，并有望复制到电力、港口、煤矿等军团业务。在机器人领域，如何规划多机器人的任务执行以实现最优调度，如何控制机器人的转向与前进速度以实现全程无碰的最优路径移动等都是非常有价值的算法难题。

概括

本次项目通过软件模拟了多机器人的运行环境以及真实机器人的状态信息。在机器人路径行走过程中，采用 $PID$ 算法控制机器人行驶，使机器人稳定行驶。在选取目标中，采用贪心算法选取最优目标。机器人在复杂地形的路径规划问题中，采用了A*算法选取最优路径，针对不同类型的地图，分别使用欧氏距离和曼哈顿距离作为启发式函数。考虑到部分机器人或者工作目标点被障碍物围死，没有路径情况下A算法时间复杂度高，因为采用DFS算法判断区域是否封闭区域。在A算法中，机器人每步决策为八个方向，步长为0.25米。为了消除A*算法路径中冗余的点，采用了算法对机器人的路径进行简化。同时，为了避免机器人之间的互相碰撞，采用DWA算法防止机器人之间互相碰撞。

具体实现

PID控制转向

在涉及到控制机器人旋转时，本项目采用PID算法进行控制，PID算法是一种常用的反馈控制算法，他通过测量系统的的当前状态和期望状态之间的误差，并对误差进行比例、积分和微分计算，从而产生控制输出。下面是 $PID$ 算法的公式表示：

u(t) = Kp×e(t) + Ki×∫e(t)dt + Kd×(de(t)/dt)

其中，$ u(t) $是控制量，$ e(t) $是误差，$ Kp $、$ Ki $、$ Kd $是比例、积分和微分系数，$ ∫ $表示积分符号，$ de(t)/dt $表示误差的变化率。

下面是 $PID$ 算法控制机器人旋转的具体实现步骤：

设定目标旋转角度$ θd $和当前旋转角度$ θ$。
计算误差e =。
计算误差的积分项 $I：I = I + e*dt$ ，其中 $dt$ 是控制周期， $I$ 表示累计误差。
计算误差的微分项 $D：D = (e - e_p)/dt$ ，其中 $e_p$ 是上一次的误差， $D$ 表示误差变化率。
计算控制量 $u：u = Kp×e + Ki×I + Kd×D$ ，其中 $Kp$ 、 $Ki$ 和 $Kd$ 是比例、积分和微分系数。
将控制量 $u$ 应用到机器人旋转控制系统中，例如，通过调整电机转速或调整舵机角度等。
重复执行步骤2到6，直到机器人旋转到目标角度。

以上步骤的具体实现中，比例系数 $Kp$ 控制误差的大小，积分系数 $Ki$ 控制误差的积累，微分系数 $Kd$ 控制误差的变化率。经过大量的实验以及调试，选取了最优的系数以达到最优的控制效果。

目标选取

在云智能机器人协同调度优化问题中，目的是控制机器人前往各个工作台进行商品的购买、出售以达到最多的资金。在地图中，共有 $K$ 个工作台，工作台型号有 $1-9$ 种。有 $1-7$ 七中商品。其中 $1-3$ 号生产 $1-3$ 号商品， $4-7$ 号工作台收购其他商品并加工成 $4-7$ 号商品。 $8、9$ 号工作台只收购各种商品，不进行出售。已经商品 $1-7$ 的价值 $V_i$ 考虑到最优目标选取计算量大，机器人可能无法及时做出反应，因为本文采用贪心算法进行目标选取。机器人 $R_j$ 每次任务更新，只考虑机器人前往 $m(m<=K)$ 号工作台购买 $i$ 号商品，接着前往 $n(n<=K)$ 号工作台将 $i$ 号商品出售，从而获取利益 $V_i$ 。
最终确定价值指标:

V_c=(W_1×Value_1+W_2×Value_2)/(D_{jm}+D_{mn})

其中 $W_1、W_2$ 是两个价值的权重。 $Value_1$ 表示工作台 $m$ 生产的 $i$ 号商品的本身价格， $Value_2$ 表示工作台 $n$ 生产的商品的潜在价格， $Value_2$ 的存在表示，将商品买到指定工作台获取的价值不仅仅是商品本身的价值，还包括了将商品买到指定工作台之后，制定工作台将该商品加工成价格更高的商品。

A*路径规划

机器人路径规划问题中，A*算法是常用的算法。在云智能机器人协同调度优化问题中，采用A*算法对机器人路径优化问题求解步骤如下：

定义问题：路径的起点定义为机器人的当前位置，路径的终点为机器人目标工作台的位置。当机器人距离工作台小于0.4米视为到达目标点。
初始化：将起点放入 $open$ 列表，并设置其 $f$ 值为起点到终点的估价函数值。将其 $g$ 值设为0。设置 $f=g+h$ ,在本项目中 $g$ 表示起点到当前位置的欧式距离。 $h$ 根据地图的不同选取不同的启发式函数，较为复杂，障碍物杂乱的地图中使用欧式距离作为启发式函数：

h=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

在类似城市道路的地图，如由横线与竖线划分房间的图采用曼哈顿距离作为启发式函数：

h=|x_2-x_1|+|y_2-y_1|

循环执行以下操作：
a. 从 $open$ 列表中找到 $f$ 值最小的节点，将其作为当前节点，并将其从 $open$ 列表中删除，加入到 $close$ 列表中。
b. 如果当前节点是终点，则搜索结束，返回路径。
c. 生成当前节点的所有子节点，并计算它们的f值和g值。如果子节点已经在 $close$ 列表中，则跳过。
d. 如果子节点不在 $open$ 列表中，则将其加入 $open$ 列表中。
e. 如果子节点已经在 $open$ 列表中，比较当前路径与新路径的 $g$ 值，如果新路径的 $g$ 值更小，则更新该节点的父节点和 $g$ 值。
如果 $open$ 列表为空，表示没有找到路径，算法结束。
A*查找路效果如下：

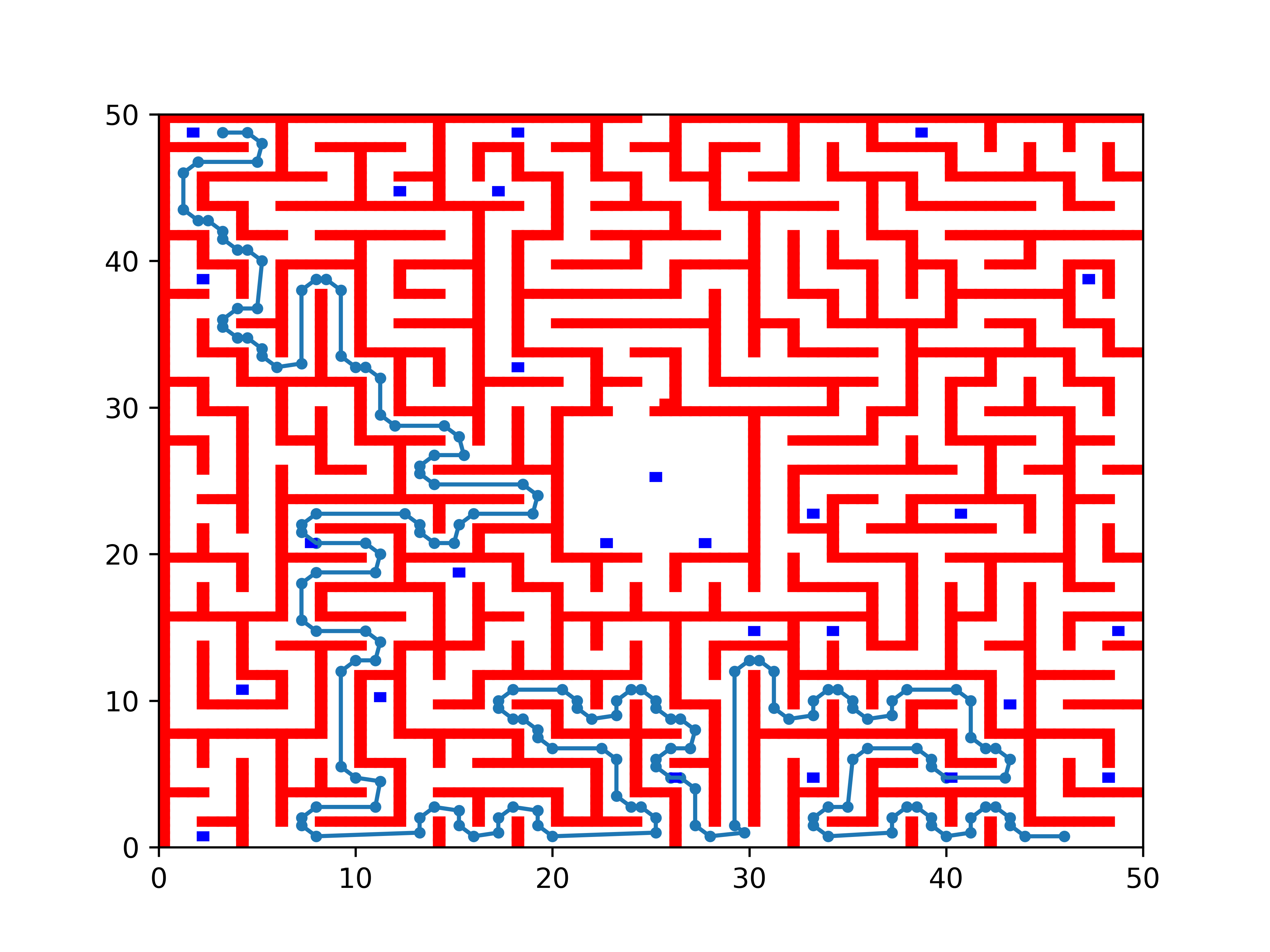
$Douglas-Peucker$ 路径简化

在使用A*算法找出路径之后，由于步长为0.25米，因此在路径中会出现非常多的点或者波动，导致机器人在行驶时速度慢并且不稳定，因此使用 $Douglas-Peucker$ 算法对路径简化。具体步骤为：

将输入的路径抽象为一个点集合。
从点集合中选择一个起点和终点，构建一条直线段。
遍历点集合中的每一个点，并计算该点到直线段的距离。找到距离最大的点，记作 $dmax$ 。其中 $d$
$d = |(B-A) × (C-A)| / |B-A|$ $dmax = max(|(P-A) × (B-A)| / |B-A|, |(P-B) × (A-B)| / |A-B|)$
如果 $dmax$ 小于设定的阈值，则跳转到步骤7，否则继续执行。
将 $dmax$ 对应的点作为拐点，将点集合分为两个子集，分别对每个子集递归执行步骤2到步骤5，直到所有的点都被处理。
将所有的子集合并起来，得到简化后的路径。
算法结束。
对于未优化的路径如下图:

$Douglas-Peucker$ 算法优化后的路径如下：

$DWA$ 防碰撞

$DWA$ 算法（Dynamic Window Approach）是一种基于动态窗口的机器人路径规划算法，可以用于避免机器人与障碍物的碰撞。以下是 $DWA$ 算法的一些基本步骤和公式：

1.获取机器人当前状态

假设机器人当前位置为 $(x, y, \theta)$ ，其中 $x$ 和 $y$ 分别表示机器人在水平和垂直方向上的坐标， $\theta$ 表示机器人的朝向角度。

2.生成速度样本

在 $DWA$ 算法中，机器人可以采取不同的速度和角速度，因此需要生成速度样本。可以通过设定速度和角速度的最大和最小值来限制样本范围。

假设最大速度为 $v_{max}$ ，最小速度为 $v_{min}$ ，最大角速度为 $\omega_{max}$ ，最小角速度为 $\omega_{min}$ ，那么可以生成速度样本：

V=[v_{min},v_{min}+Δv,⋯,v_{max}]

ω=[ω_{min},ω_{min}+Δω,⋯,ω_{max}]

其中 $\Delta v$ 和 $\Delta \omega$ 分别表示速度和角速度的步长。

3.计算代价函数

在 $DWA$ 算法中，代价函数用于评估每个速度样本的优劣程度，从而选择最优的速度样本。代价函数通常包括两部分：一是路径跟随误差，二是碰撞风险。

路径跟随误差

假设机器人当前位置为 $(x, y, \theta)$ ，速度样本为 $(v, \omega)$ ，那么可以通过计算机器人在下一时刻的位置 $(x', y', \theta')$ 来评估路径跟随误差。这里可以使用机器人运动学模型进行预测。

假设 $\Delta t$ 表示下一时刻的时间间隔，那么机器人在下一时刻的位置可以表示为：

x' = x + v * cos(θ) * Δt

y' = y + v * sin(θ) * Δt

θ ’=θ +ωΔt

路径跟随误差可以通过计算当前位置和目标位置之间的距离来表示：

d_{goal} = \sqrt{(x' - x_{goal})^2 + (y' - y_{goal})^2}

其中 $(x_{goal}, y_{goal})$ 表示目标位置的坐标。

碰撞风险

为了避免机器人与障碍物的碰撞，需要计算机器人行进路径上的碰撞风险。可以使用机器人的传感器获取周围障碍物的信息，比如障碍物的位置和尺寸等。然后可以通过计算机器人运动轨迹上每个位置的碰撞风险来评估当前速度样本的安全性。一种常见的方法是使用高斯分布模型来表示碰撞风险，具体计算公式如下：

(x,y) = \frac{\sigma_{obs}}{2\pi} \exp \left(-2\sigma_{obs}^2 d_{obs}^2(x,y)\right)

其中 $d_{obs}(x,y)$ 表示机器人当前位置和路径上位置 $(x,y)$ 之间的最小障碍物距离， $\sigma_{obs}$ 表示障碍物的标准差，可以看作是一个控制碰撞风险扩散程度的参数。在实际应用中，可以根据具体情况调整该参数。

4.选择最优速度样本

通过计算代价函数，可以评估每个速度样本的优劣程度，从而选择最优的速度样本。一种常见的方法是将代价函数分为两部分，分别表示路径跟随误差和碰撞风险。然后通过加权求和得到最终的代价函数，具体计算公式如下：

J(v,\omega) = \alpha d_{goal} + \beta p_{obs}(x',y')

其中 $\alpha$ 和 $\beta$ 表示路径跟随误差和碰撞风险的权重系数，可以根据实际应用进行调整。然后可以选择代价函数最小的速度样本作为最优速度样本。

5.执行路径规划

选择最优速度样本后，可以使用机器人运动学模型进行路径规划。假设机器人当前位置为 $(x, y, \theta)$ ，最优速度样本为 $(v^*, \omega^*)$ ，那么机器人在下一时刻的位置可以表示为：

x' = x + v \cdot \cos(\theta) \cdot \Delta t

y' = y + v \cdot \sin(\theta) \cdot \Delta t

\theta' = \theta + \omega \cdot \Delta t

然后可以将机器人移动到下一时刻的位置 $(x', y', \theta')$ ，并将其作为新的起点进行下一轮路径规划。

初赛部分

初赛代码链接

https://github.com/xhsioi/huawei_robot

赛事时间安排

区域初赛	区域复赛	总决赛
3.10赛题发布	3.29赛题发布	4.10赛题发布
3.24报名截止	4.9现场复赛	4.22现场总决赛
3.26提交截止	4.10公布晋级名单
3.27-3.28公布晋级名单

团队合作情况

我们团队共三人。

我们团队使用了飞书进行线上合作，包括任务安排的分工表格、当前问题陈述、每次会议纪要等等。

我们团队的源码管理则使用了git版本管理，基本上每天都有小迭代，三天一个大改进。

每日会议

每天中午或晚上进行比赛的会议讨论，主要有以下内容：

陈述自己新编写的代码的功能，让团队成员理解作用和如何配合使用
讨论当前遇到了什么问题，以及如何解决
讨论从结束会议到下一次会议开始，如何合理分工

分工合作

我的工作基本有如下几点：

前期构建pid算法，制作出防碰撞的雏形；

def control_to_goal(bots, bot, target1, isfinish, start_loc):
    direction1 = (target1 - bot.pos) / np.linalg.norm(target1 - bot.pos)  # 计算机器人到目标点的方向向量
    direction_right1 = math.atan2(direction1[1][0], direction1[0][0])  # 计算夹角
    ori = bot.toward
    dis = np.linalg.norm(bot.pos - target1)
    err = direction_right1 - ori
    while err > math.pi:
        err -= 2.0 * math.pi
    while err < -math.pi:
        err += 2.0 * math.pi
    # print(ori,direction_right1,err, file=sys.stderr)
    robot_start = np.array([[start_loc[bot.id - 1][0]], [start_loc[bot.id - 1][1]]])
    # if np.linalg.norm(bot.pos - target1) <6/math.pi*2:
    #     robot_control("forward", bot.id-1, np.linalg.norm(bot.pos - target1)/math.pi)
    #     robot_control("rotate", bot.id-1, err*1000000)
    start_to_tar = np.linalg.norm(robot_start - target1)
    r_sei = math.pi / 2 - (err)
    r = dis / 2 / math.cos(r_sei)

    turn_flag[bot.id-1] = True
    for i in range(4):
        if i != bot.id - 1:
            p1 = np.array([bot.x, bot.y])
            p2 = np.array([bots[i].x, bots[i].y])
            v1 = np.array([bot.linear_v_x, bot.linear_v_y])
            v2 = np.array([bots[i].linear_v_x, bots[i].linear_v_y])
            p = p1 - p2
            v = v1 - v2
            theta = np.arccos(np.dot(p, v) / np.linalg.norm(p) * np.linalg.norm(v))
            t = np.fabs(np.dot(p, v) / np.dot(v, v))
            p_collide = p1 + v1 * t
            if theta < np.pi/2:
                if t < 0.05 and not turn_flag[bots[i].id-1]:
                    theta1 = bot.toward - bots[i].toward
                    if np.sin(theta1) > 0:
                        robot_control("forward", bot.id - 1, 6)
                        robot_control("rotate", bot.id - 1, 6 / r+np.pi/2)
                    else:
                        robot_control("forward", bot.id - 1, 6)
                        robot_control("rotate", bot.id - 1, 6 / r-np.pi/2)
                    return
                elif t < 0.1 and not turn_flag[bots[i].id-1]:
                    theta1 = bot.toward - bots[i].toward
                    if np.sin(theta1) > 0:
                        robot_control("forward", bot.id - 1, 6)
                        robot_control("rotate", bot.id - 1, 6 / r+np.pi / 4)
                    else:
                        robot_control("forward", bot.id - 1, 6)
                        robot_control("rotate", bot.id - 1, 6 / r-np.pi / 4)
                    return
                elif t < 0.2 and not turn_flag[bots[i].id-1]:
                    theta1 = bot.toward - bots[i].toward
                    if np.sin(theta1) > 0:
                        robot_control("forward", bot.id - 1, 5)
                        robot_control("rotate", bot.id - 1, 6 / r+np.pi / 8)
                    else:
                        robot_control("forward", bot.id - 1, 5)
                        robot_control("rotate", bot.id - 1, 6 / r-np.pi / 8)
                    return
    if target1[0][0] < 1 or target1[0][0] > 49 or target1[1][0] < 1 or target1[1][0] > 49:
        if dis < 0.8:
            robot_control("forward", bot.id - 1, 2)
        elif dis < 1.5:
            robot_control("forward", bot.id - 1, 4)

        else:
            if abs(err) > math.pi / 6:
                robot_control("forward", bot.id - 1, 6)
                robot_control("rotate", bot.id - 1, err * 1000000)
            else:
                r_sei = math.pi / 2 - err
                r = dis / 2 / math.cos(r_sei)
                robot_control("forward", bot.id - 1, 6)
                robot_control("rotate", bot.id - 1, 6 / r)
    elif robot_start[0][0] < 1.5 or robot_start[0][0] > 48.5 or robot_start[1][0] < 1.5 or robot_start[1][0] > 48.5:
        # print("id",bot.id,robot_start[0][0],robot_start[1][0], "\n", file=sys.stderr)
        if np.linalg.norm(robot_start - bot.pos) < 1:

            if abs(err) > math.pi / 2:
                robot_control("forward", bot.id - 1, -1)
                robot_control("rotate", bot.id - 1, err * 1000000)
            elif abs(err) > math.pi / 6:
                robot_control("forward", bot.id - 1, 4)
                robot_control("rotate", bot.id - 1, err * 1000000)
        else:
            if abs(err) > math.pi / 6:
                robot_control("forward", bot.id - 1, 6)
                robot_control("rotate", bot.id - 1, err * 1000000)
            else:
                r_sei = math.pi / 2 - (err)
                r = dis / 2 / math.cos(r_sei)
                robot_control("forward", bot.id - 1, 6)

                robot_control("rotate", bot.id - 1, 6 / r)
    else:
        if start_to_tar / 2 < 6 / math.pi:
            #     # if abs(err) > math.pi/ 2:
            if abs(err) > math.pi / 6:
                robot_control("forward", bot.id - 1, start_to_tar / 2.5 * math.pi)
                robot_control("rotate", bot.id - 1, err * 1000000)
            else:
                r_sei = math.pi / 2 - (err)
                r = dis / 2 / math.cos(r_sei)
                robot_control("forward", bot.id - 1, 5)

                robot_control("rotate", bot.id - 1, 5 / r)
        else:
            if abs(err) > math.pi / 6:
                robot_control("forward", bot.id - 1, 6)
                robot_control("rotate", bot.id - 1, err * 1000000)
            else:
                r_sei = math.pi / 2 - (err)
                r = dis / 2 / math.cos(r_sei)
                robot_control("forward", bot.id - 1, 6)

                robot_control("rotate", bot.id - 1, 6 / r)

研究防碰撞的多种情况；
对价值系数进行动态调整，根据地图变化给出不同的参数；
对整体代码进行重构，优化代码结构；

比赛成果

初赛练习赛 - rk15

初赛正式赛 - rk7

比赛体验与感受

对于赛题

虽然是我第一次打华为的软挑比赛（之前已经办了八届好像），但是这个比赛设置的场景确实比较复杂了，出题人能设计出这种场景和限制，并写出整个系统的可执行代码，然后在这个框架下让选手自由发挥，已经很厉害了。赛题兼具挑战性、复杂性和趣味性，赛题自由度很大，能够激发思维缜密的解决方案，也能够容纳天马行空的开创性想法。而且比赛的背景并没有脱离实际，是机器人集群的复杂决策问题和控制论，与ros等相关。

还有一个亮点，就是针对安全问题专门进行了防护：由于判题是选手提交源代码程序放在服务器上运行，选手有可能上传恶意代码在服务器执行。针对这个问题，官方规定python方面只允许numpy库的使用，同时不允许创建奇奇怪怪的文件类型等等，防止选手进行破坏服务器的一系列操作（虽然不知道是否真的做了这么严密的防护，但是有这个意识是好的）

对于团队合作

这次意识到团队合作的重要性，我们做的还是远远不够。如果写出来的代码无注释，变量随意命名，代码结构不分模块全放在main.py，代码版本管理混乱…那么真是三个人各写各的，只有自己的代码自己能看得懂，别人根本别想看懂，然后各自的模块也互相嵌不进去。同时需求文档的编写也很重要，否则三个人造三次轮子，这轮子各自长得还不一样（函数参数不同，返回值也不同，代码中的位置也不同，或者甚至硬编码在主文件中…）。

复赛部分

复赛代码链接

https://github.com/xhsioi/huawei_robot_2

团队合作情况

本次复赛我们仍旧采用敏捷团队开发，使用git进行代码提交，每个成员建立自己的分支，每天至少commit一次，每三天至少进行一次merge。

每日站立会议

每天都会在A区三楼进行站立会议，讨论各自的开发进度。对于我而言，我的任务是对机器人的行走控制模块进行处理，以及防碰撞部分的开发（最后只开发出了较为完善的防碰撞、防撞死，部分情况没有考虑到）。

阐述自己开发的各个模块接口的作用，进行简单的调试，根据各自的需求简单对接口参数进行调整。
讨论当前模块的开发遇到的一些问题，对于必要的问题集中处理。本次比赛中，我的机器人行走速度、转弯控制模块就是通过我和高两人联合开发完成的。
讨论从结束会议到下一次会议开始，如何合理分工，确定下一次会议之前需要达到的目标；

分工合作

我的工作基本上由以下的几个点构成：

机器人控制模块的应用开发，定义机器人在前往取货点、前往出货点的控制算法，使机器人在有墙壁的情况下行动路线更加顺滑，减少碰撞的行走。

#实现对机器人的控制，包括到达目标点、防止撞墙撞死、防止对撞撞死
def control_to_goal(game_map_array, bots, path, bot0_status, index):
    Single_robot = bots[index]
    connect_set = [-1, 1]
    # 如果不存在路径，保持静止状态
    if path[index][0][0] == 0:
        robot_control("rotate", Single_robot.id - 1, 0)
        robot_control("forward", Single_robot.id - 1, 0)
        return bot0_status
    # 当路径上存在目标，进行直行、旋转、防撞死等操作
    else:
        bot0_status_i = int(bot0_status[index])
        target1 = np.array(
            [path[index][min(len(path[index]) - 1, bot0_status_i)][0],
             path[index][min(len(path[index]) - 1, bot0_status_i)][1]])
        direction1 = (target1 - Single_robot.pos) / np.linalg.norm(target1 - Single_robot.pos)  # 计算机器人到目标点的方向向量
        direction_right1 = math.atan2(direction1[1], direction1[0])  # 机器人到目标点的夹角
        ori = Single_robot.toward  # 机器人当前朝向
        dis = np.linalg.norm(Single_robot.pos - target1)  # 计算机器人到目标点的距离
        err = direction_right1 - ori  # 计算机器人到目标点的夹角和机器人当前朝向的误差
        while err > math.pi:
            err -= 2.0 * math.pi
        while err < -math.pi:
            err += 2.0 * math.pi
        r_sei = math.pi / 2 - err
        r = dis / 2 / math.cos(r_sei)

        # 防止撞在墙上不能动
        if location_count[index] == coun:
            bot_location[index][0] = bots[index].x
            bot_location[index][1] = bots[index].y
            location_count[index] = 0
        location_count[index] = location_count[index] + 1
        if bot_location[index][0] != 0 and bot_location[index][1] != 0 and distance(Point(bots[index].x, bots[index].y),                                                                                  1])) < 0.01 and \
                location_count[index] == coun:
            bot0_status[index] = max(bot0_status[index] - 1, 0)
            robot_control("forward",bots[index].id-1 , -2)
            return bot0_status
        if dis < 0.1:
            bot0_status[index] = bot0_status_i + 
        print("target:",target1,bots[index].id,file=sys.stderr)

        if dis<1:
            if abs(err) > math.pi / 4 :
                robot_control("forward", Single_robot.id - 1, -1)
                robot_control("rotate", Single_robot.id - 1, err*10)
            elif abs(err) > math.pi / 18:
                robot_control("forward", Single_robot.id - 1, -0.1)
                robot_control("rotate", Single_robot.id - 1, err*10)
            else:
                r_sei = math.pi / 2 - err
                r = dis / 2 / math.cos(r_sei)
                if 2/r>math.pi:
                    w=math.pi/4
                    v=w*r
                    robot_control("forward", Single_robot.id - 1, v)
                    robot_control("rotate", Single_robot.id - 1, w)
                else:                    
                    #                 return bot0_status
                    v=2
                    w=v/r
                    
                    robot_control("forward", Single_robot.id - 1, v)
                    robot_control("rotate", Single_robot.id - 1, w)
        else:
            if abs(err) > math.pi / 4:
                robot_control("forward", Single_robot.id - 1, -1)
                robot_control("rotate", Single_robot.id - 1, err*10)
            elif abs(err) > math.pi / 18:
                robot_control("forward", Single_robot.id - 1, -0.1)
                robot_control("rotate", Single_robot.id - 1, err*10)
            else:
                r_sei = math.pi / 2 - err
                r = dis / 2 / math.cos(r_sei)
                if 6/r>math.pi:
                    w=math.pi/2
                    v=w*r
                    robot_control("forward", Single_robot.id - 1, v)
                    robot_control("rotate", Single_robot.id - 1, w)
                else:                    
                    #                 return bot0_status
                    w=6/r
                    v=6
                    robot_control("forward", Single_robot.id - 1, v)
                    robot_control("rotate", Single_robot.id - 1, w)

    return bot0_status

由于路径算法发生改变，路径被分解成起点、终点和过程中的拐点，设计算法确定如何筛除多余的拐点，让拐点数量和碰撞次数达到一个平衡状态。

def simplify_path(points, tolerance):
    """
    使用Douglas-Peucker算法对路径进行简化
    """
    if len(points) < 3:
        return points

    # 找到路径上距离起点和终点最远的点
    d_max = 0
    index = 0
    end = len(points) - 1
    for i in range(1, end):
        d = perpendicular_distance(points[i], points[0], points[end])
        if d > d_max:
            index = i
            d_max = d

    # 如果最远点的距离小于阈值，则直接连接起点和终点
    if d_max < tolerance:
        return [points[0], points[end]]

    # 递归地对路径的左右两部分进行简化
    left = simplify_path(points[:index+1], tolerance)
    right = simplify_path(points[index:], tolerance)

    # 返回简化后的路径
    return left[:-1] + right

对于撞死问题，我分成两球撞死和墙撞死两种情况进行考虑，其中求撞死还需要考虑特殊情况的撞死（即与墙壁相关的两球撞死

#防止两个机器人对撞撞死
for j in range(4):
        if j != bots[index].id - 1 and type(path[j]) is list:
            if j > index:
                connect_set = [-1, 1]
            else:
                connect_set = [1, -1]
            # 判断两个向量是否相交：
            ii = int(bot0_status[index])
            jj = int(bot0_status[j])
            p1 = Point(bots[index].x, bots[index].y)
            p3 = Point(bots[j].x, bots[j].y)
            p2 = Point(path[index][min(len(path[index]) - 1, ii)][0], path[index][min(len(path[index]) - 1, ii)][1])
            p4 = Point(path[bots[j].id - 1][min(len(path[j]) - 1, jj)][0],
                       path[bots[j].id - 1][min(len(path[j]) - 1, jj)][1])
            # 判断两个机器人之间的距离,出现对撞后进行避让
            if distance(p1, p3) <= 1.10 and index < j:
                robot_control("forward" , bots[index].id-1 , -2)
                robot_control("rotate", bots[index].id - 1, np.pi/6)
                return bot0_status
            if intersection(p1, p3, p2, p4):
                # 求交点
                px = ((p1.x * p2.y - p1.y * p2.x) * (p3.x - p4.x) - (p1.x - p2.x) * (p3.x * p4.y - p3.y * p4.x)) / (
                        (p1.x - p2.x) * (p3.y - p4.y) - (p1.y - p2.y) * (p3.x - p4.x))
                py = ((p1.x * p2.y - p1.y * p2.x) * (p3.y - p4.y) - (p1.y - p2.y) * (p3.x * p4.y - p3.y * p4.x)) / (
                        (p1.x - p2.x) * (p3.y - p4.y) - (p1.y - p2.y) * (p3.x - p4.x))
                intersect = Point(px, py)
                # 判断交点是否在路径上
                if (math.fabs(dot(p2-p1,p4-p3)) > 0.8*distance(p2-p1 , Point(0,0))*distance(p4-p3 , Point(0,0))) and distance(p1, p3) < 2 and index < j:
                    robot_control("forward", bots[index].id - 1, -2)
                    robot_control("rotate", bots[index].id - 1, connect_set[0] * np.pi)
                    return bot0_status
                if distance(intersect, p1) < 4 and distance(intersect, p3) < 2 and index < j:
                    robot_control("forward", bots[index].id - 1, -2)
                    robot_control("rotate", bots[index].id - 1, connect_set[0] * np.pi)
                    return bot0_status
# 防止撞在墙上不能动
        if location_count[index] == coun:
            bot_location[index][0] = bots[index].x
            bot_location[index][1] = bots[index].y
            location_count[index] = 0
        location_count[index] = location_count[index] + 1
        if bot_location[index][0] != 0 and bot_location[index][1] != 0 and distance(Point(bots[index].x, bots[index].y),                                                                                  1])) < 0.01 and \
                location_count[index] == coun:
            bot0_status[index] = max(bot0_status[index] - 1, 0)
            robot_control("forward",bots[index].id-1 , -2)
            return bot0_status
        if dis < 0.1:
            bot0_status[index] = bot0_status_i + 
        print("target:",target1,bots[index].id,file=sys.stderr)

比赛成果

北京华为研究所复赛前五强，遗憾没能参加总决赛，薅了华为的羊毛。

比赛体验与感受

对于赛题

在复赛过程中，业务场景再次发生了变化，可以清楚地看到业务更加贴近实际：墙壁的阻碍，移动的其他机器人的阻碍，躲避算法的开发无疑是本次复赛的重点。说来惭愧，我从复赛就开始进行关于pid算法的研究，最终发现判题器设置的转速足够支撑转动方向的稳定。我们通过反复尝试，从pid三项参数、移动的分段处理等多个方面进行行走的优化，发现都不如在机器人完成某种操作后立刻停止，保持0线速度转动寻找方向的解决方案。最后，利用分段和新增墙壁来对残缺的避让算法进行补救，算是完成了这部分算法的最后优化。