每日一题整理——2023.3

2023.1.3

矩阵中的局部最大值

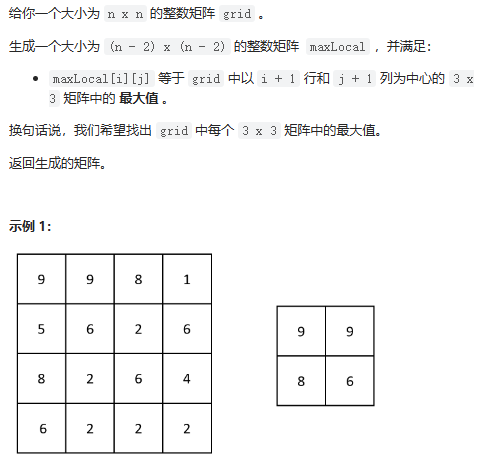
数据范围：

我的思路：暴力模拟，做的依托答辩

class Solution {
public:
    vector<vector<int>> largestLocal(vector<vector<int>>& grid) {
        int n = grid[0].size();
        vector<vector<int>> res(n-2,vector<int>(n-2));
        int max;
        for(int i=0;i<n-2;i++){
            for(int j = 0; j < n-2 ; j++){
                max = 0;
                for(int ii = i ; ii < 3 + i; ii++){
                    for(int jj = j ; jj < 3 + j ; jj++ ){
                        if(grid[ii][jj] > max){
                            max = grid[ii][jj];
                        }
                    }
                }
                res[i][j]=max;
            }
        }
        return res;
    }
};

最大池化，没有最优解法，只有暴力模拟；

2023.3.2

String Compression

数据范围：

我的思路：

参数i记录结果字符串的末尾位置；参数j记录当前字符串的遍历位置，count进行计数，需要考虑字符串向整形数字的变化：

class Solution {
public:
    int compress(vector<char>& chars) {
        int n = chars.size();
        if(n == 1){
            return 1;
        }
        int i = 0;
        int j = 0;
        while(j<n){
            int count = 1;
            while(j<n-1 && chars[j] == chars[j+1]){
                count++;
                j++;
            }
            chars[i++] = chars[j++];
            if(count > 1){
                string s = to_string(count);
                for(char c : s){
                    chars[i++] = c;
                }
            }
            count = 1;
        }
        return i;
    }
};

2023.3.3

Find the Index of the First Occurrence in a String

数据范围：

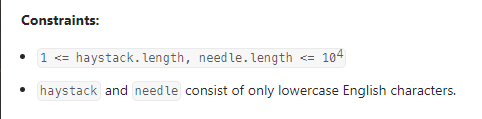
我的思路：

利用kmp算法，构建next数组对子串进行记录，得到如下结果：重点是next数组的构建：

class Solution {
public:
    int strStr(string haystack, string needle) {
        int m = haystack.length();
        int n = needle.length();
        vector<int> next(n,0);
        int res = -1;
        if(m<n){
            return res;
        }
        if(n==1){
            for(int ii = 0 ;ii<m;ii++){
                if(haystack[ii] == needle[0]){
                    return ii;
                }
            }
            return res;
        }
        next[0] = -1;
        next[1] = 0;
        int k = 0;
        int j = 2;
        while(j < n){
            if(k == -1 || needle[j-1] == needle[k]){
                next[j] = k + 1;
                k++;
                j++;
            }
            else{
                k = next[k];
            }
        }
        int i = 0;
        j = 0;
        while(i<m){
            if(haystack[i] == needle[j]){
                i++;
                j++;
                if(j == n){
                    res = i - n;
                    break;
                }
            }
            else{
                j = next[j];
                if(j == -1){
                    j = 0;
                    i++;
                }
            }
        }
        return res;
    }
};

2023.3.4

Count Subarrays With Fixed Bounds

数据范围：

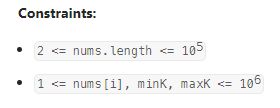
我的思路：

数据类型分为3种，等于最小值、等于最大值、都不相等；

我们需要计算的是最小值和都不相等的区间，或者是最大值和都不相等的区间，这两方面都需要考虑；最终使用滑动窗口进行计算，代码如下：

class Solution {
public:
    long long max(long long a , long long b){
        return a > b ? a : b;
    }
    long long countSubarrays(vector<int>& nums, int minK, int maxK) {
        long res = 0;
        long jbad = -1;
        long jmin = -1;
        long jmax = -1;
        long n = nums.size();
        for(int i = 0 ; i < n ; i++){
            if(nums[i] < minK || nums[i] > maxK){
                jbad = i;
            }
            if(nums[i] == minK){
                jmin = i;
            }
            if(nums[i] == maxK){
                jmax = i;
            }
            res = res + max(0,min(jmin,jmax) - jbad);
        }
        return res;
    }
};

2023.3.6

Kth Missing Positive Number

数据范围：

我的思路：

首先想到的就是用数组储存每个间隔中存在的数字个数，然后利用间隔取数。但是这里出现了一些问题，就是两端的取值问题。这里我首先对长度为1的数组进行特殊处理，然后存储间隔数量，然后对数组进行第二次筛选，将两侧的数组进行分割，最后再对间隔进行遍历，得到如下的程序：

class Solution {
public:
    int findKthPositive(vector<int>& arr, int k) {
        int n;
        n = arr.size();
        if(n == 1){
            if(arr[0] == 1){
                return k + 1;
            }
            return k > arr[0] ? (k-1) : k;
        }
        vector<int> temp(n);
        int i,sum=0;
        int res = 0;
        for(i = 0 ; i < n ; i++){
            temp[i] = arr[i] - res - 1;
            res = arr[i];
            sum += temp[i];
        }
        if(k > sum){
            return (arr[n-1] + k - sum);
        }
        if(k <= temp[0]){
            return k;
        }
        for(i = 0 ; i < n ; i++){
            if(k <= temp[i]){
                return (arr[i-1] + k);
            }
            else{
                k = k - temp[i];
            }
        }
        return -1;
    }
};

评论区中的题解：

int findKthPositive(vector<int>& arr, int k) {
    int lo = 0, hi = arr.size();
    while (lo < hi) {
        int mid = lo + (hi - lo) / 2;
        if (arr[mid] - mid > k) hi = mid;
        else lo = mid + 1;
    }
    return lo + k;
}

原来二分就可以啊，麻了；

2023.3.7

Minimum Time to Complete Trips

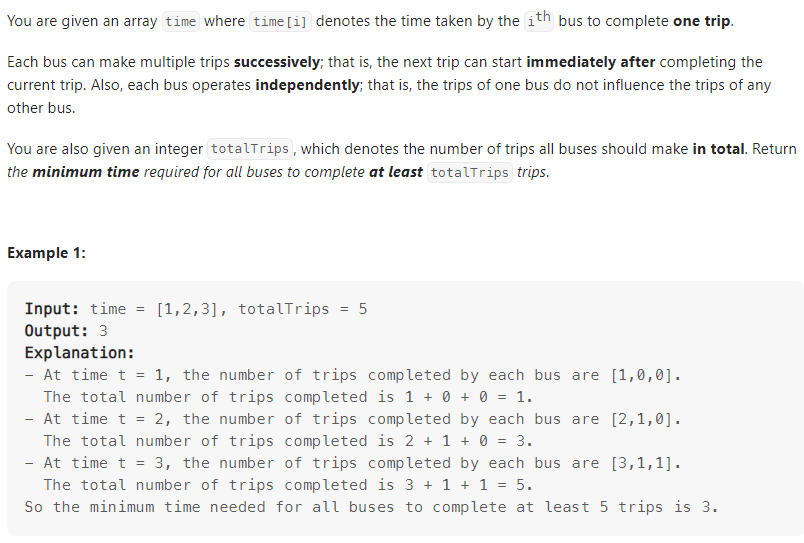
数据范围：

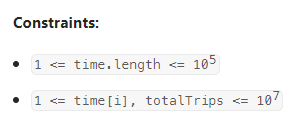
我的思路：

上来就是一个简单模拟，啪的一下很快啊，直接TL；

最后看了评论区的方法，找到了logn的解法：既然返回值是执行的时间，时间也是呈现递增变化的数量，因此使用二分法对数据进行求解，最终不断收敛确定trip的值，代码如下：

#define ll long long 
class Solution {
public:
    long long minimumTime(vector<int>& time, int totalTrips) {
        ll start = 1;
        ll end = 1e14;
        while(start <= end){
            ll trip = 0;
            ll mid = start + (end - start)/2;
            for(int i=0;i<time.size();i++)
                trip += mid / time[i];
            if(trip < totalTrips){
                start = mid + 1;
            }
            else 
                end = mid - 1;
        }
        return start;
    }
};

初始状态下，作者规定了最大边界和最小边界，然后利用二分法逐步逼近最优方案；

2023.3.8

Koko Eating Bananas

数据范围：

我的思路：

简单，二分就完事了，需要注意的点是左右指针的移动需要注意位移，right = mid + 1这里卡了我半天，此外就是对sum的计算。代码如下：

class Solution {
public:
    int minEatingSpeed(vector<int>& piles, int h) {
        int n = piles.size();
        int i;
        long sum = 0;
        int max = -1;
        int mid;
        for(i = 0 ; i < n ; i++){
            if(piles[i] > max){
                max = piles[i];
            }
        }
        int left = 1;
        int right = max;
        while(left < right){
            mid = (left + right) / 2;
            sum = 0;
            for(i = 0 ; i < n ; i++){
                sum = sum + (piles[i] - 1) / mid + 1;
            }
            if(sum <= h){
                right = mid;
            }
            else if(sum > h){
                left = mid + 1;
            }
        }
        return left;
    }
};

2023.3.9

Linked List Cycle II

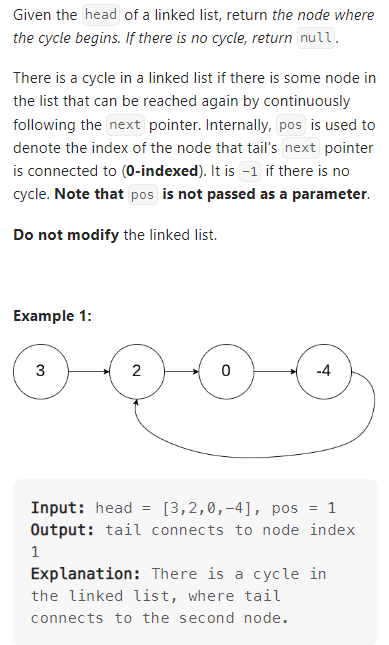
数据范围：

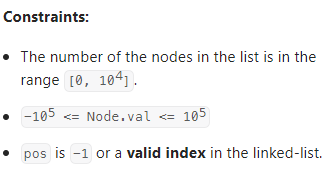
我的思路：

想着用快慢指针做，发现了判断是否有环的方法，但是没有找到确定起始节点的方法，后来发现利用快慢指针也能做，最后给出了如下的代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *h1 = head;
        ListNode *h2 = head;
        while(h2!=NULL && h2->next!=NULL){
            h1 = h1->next;
            h2 = h2->next->next;
            if(h1 == h2){
                h1 = head;
                while(h1!=h2){
                    h1 = h1->next;
                    h2 = h2->next;
                }
                return h1;
            }
        }
        return NULL;
    }
};

2023.3.10

Linked List Random Node

数据范围：

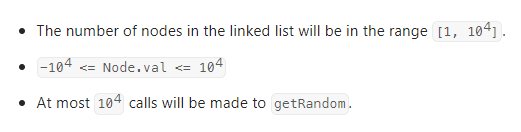
我的思路：

开始没搞懂这题的输入，正常想要随机输出链表中的一个节点的值，需要对链表进行两次遍历，即：

• 获取整个链表的长度；
• 根据长度设置随机数获取节点；

这里可以进行改进，因为对于整体自然数和固定长度的链表而言，每个节点的倍数的数量是相同的，因此我们只需要进行一次遍历即可：向前遍历，记录当前长度，然后将随机数和当前长度做余数得出概率。代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
private:
    ListNode *h;
public:
    Solution(ListNode* head) {
        h = head;
        std::srand(std::time(0));
    }
    
    int getRandom() {
        int count = 0;
        ListNode *p = h;
        int result = p->val;
        while(p){
            count++;
            if(rand()%count==0){
                result = p->val;
            }
            p = p->next;
        }
        return result;
    }
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution* obj = new Solution(head);
 * int param_1 = obj->getRandom();
 */

2023.3.11

Convert Sorted List to Binary Search Tree

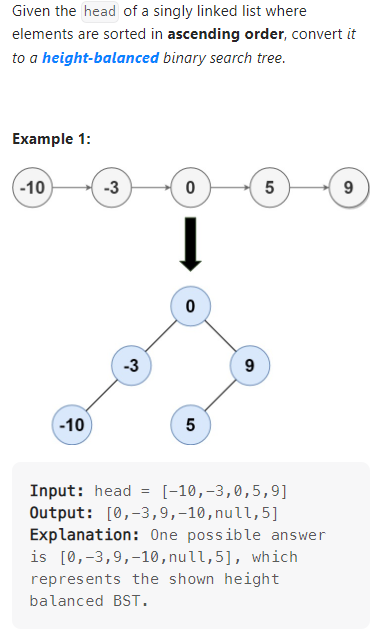
数据范围：

我的思路：

利用快慢指针找到链表的中间位置，然后取当前节点为根节点，对两侧的链表进行递归操作，得到平衡二叉树，代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructBST(ListNode *left,ListNode *right){
        if(left == right){
            return NULL;
        }
        ListNode *slow = left;
        ListNode *fast = left;
        while(fast != right && fast->next!=right){
            slow = slow->next;
            fast = fast->next->next;
        }
        TreeNode *root = new TreeNode(slow->val);
        root->left = constructBST(left,slow);
        root->right = constructBST(slow->next,right);
        return root;
    }
    TreeNode* sortedListToBST(ListNode* head) {
        if(head == NULL){
            return NULL;
        }
        TreeNode *root = constructBST(head,NULL);
        return root;
    }
};

2023.3.12

Merge k Sorted Lists

数据范围：

我的思路：

首先。这道题说的是多个有序链表合成一个有序列表，我觉得一眼先合并后排列，想到了二分，借鉴了评论区的思路，原来可以这么搞，用归并分割完成后每一部分进行两两排序，获得左右两个链表后再合并。具体的代码如下：

class Solution {
public:
    ListNode* merge_mid(ListNode* left , ListNode* right){
        ListNode *root = new ListNode(0);
        ListNode *tail = root;
        while(left && right){
            if(left->val < right->val){
                tail->next = left;
                left = left->next;
            }
            else{
                tail->next = right;
                right = right->next;
            }
            tail = tail->next;
        }
        tail->next = left ? left : right;
        return root->next;
    }
    ListNode* mid_construct(int left,int right,vector<ListNode*> lists){
        if(left == right){
            return lists[left];
        }
        if(left + 1 == right){
            return merge_mid(lists[left],lists[right]);
        }
        int mid = left + (right - left)/2;
        ListNode* start = mid_construct(left , mid , lists);
        ListNode* end = mid_construct(mid+1 , right , lists);
        return merge_mid(start,end);
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if(lists.empty()){
            return NULL;
        }    
        return mid_construct(0,lists.size()-1,lists);
    }
};

2023.3.13

Symmetric Tree

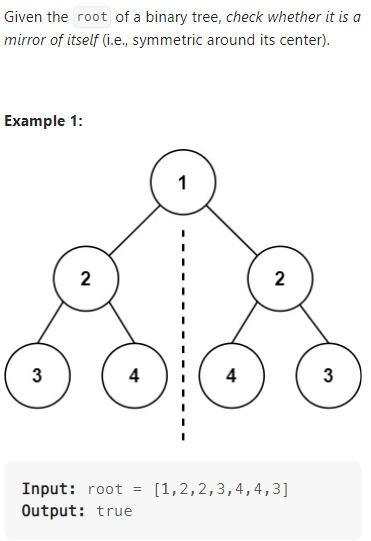
数据范围：

我的思路：

额，现在想想好像也不用递归，两边层次遍历考虑一下左右指针好像也行。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool check(TreeNode *l , TreeNode *r){
        if(l == r){
            return true;
        }
        if(l == NULL || r == NULL){
            return false;
        }
        if(l->val != r->val){
            return false;
        }
        return check(l->left,r->right) && check(l->right,r->left);
    }
    bool isSymmetric(TreeNode* root) {
        if(root->left == root->right){
            return true;
        }
        if(!root->left || !root->right){
            return false;
        }
        return check(root->left,root->right);
    }
};

2023.3.14

Sum Root to Leaf Numbers

数据范围：

我的思路：

一个dfs加回溯，还好不需要排序。但是排序也不难就是了。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sum;
    void dfs(int temp , TreeNode *root){
        temp = temp * 10 + root->val;
        if(!root->right && !root->left){
            sum+=temp;
            return;
        }
        if(root->left){
            dfs(temp,root->left);
        }
        if(root->right){
            dfs(temp,root->right);
        }
    }
    int sumNumbers(TreeNode* root) {
        sum = 0;
        dfs(0,root);
        return sum;
    }
};

2023.3.15

Submission Detail

数据范围：

我的思路：

层次遍历，当某一个节点为空时，这个节点之后就不能有节点：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        if(root==NULL){
            return true;
        }
        queue<TreeNode*> q;
        q.push(root);
        TreeNode *temp;
        bool res = false;
        while(!q.empty()){
            temp = q.front();
            q.pop();
            if(temp == NULL){
                res = true;
                continue;
            }
            if(res){
                return false;
            }
            q.push(temp->left);
            q.push(temp->right);
        }
        return true;
    }
};

2023.3.16

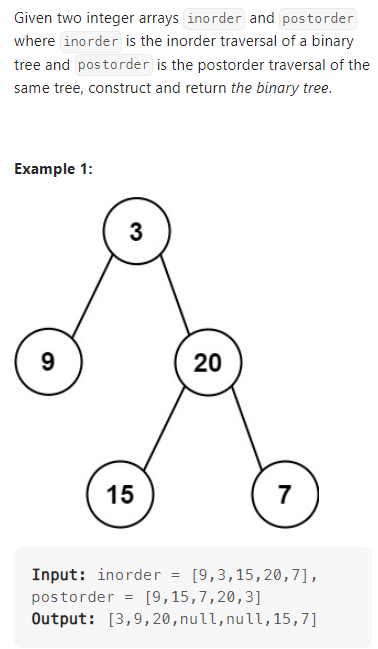
Construct Binary Tree from Inorder and Postorder Traversal

根据中序遍历和后序遍历构建二叉树；

数据范围：

我的思路：

递归，首先根据后序遍历的末尾节点确定根节点，然后在中序列表中寻找，从而将整棵树分成两部分，进而对这两部分子树进行上述操作。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    TreeNode *BuildConstruct(vector<int>& inorder , vector<int>& postorder , int l,int r,int ll,int rr,unordered_map<int,int>& index){
        if(l > r || ll > rr){
            return NULL;
        }
        int val = postorder[rr];
        TreeNode *root = new TreeNode(val);
        int temp = index[val];
        int lefttemp = temp - l;
        root->left = BuildConstruct(inorder,postorder,l,temp-1,ll,ll+lefttemp-1,index);
        root->right = BuildConstruct(inorder,postorder,temp+1,r,ll+lefttemp,rr-1,index);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        unordered_map<int,int> index;
        int i;
        for(i = 0 ; i< n ;i++){
            index[inorder[i]] = i;
        }
        return BuildConstruct(inorder,postorder,0,n-1,0,n-1,index);
    }
};

2023.3.17

Implement Trie (Prefix Tree)

构造前缀树;

数据范围：

我的思路：

没接触过类似于前缀树的构造，就我的感觉而言是一个基于dfs构造的树，用于单词查找、自动补全和拼写检查等等。前缀树的节点构造是很重要的，需要构建指向任意字母的指针和标志单词结束的表示符。具体的代码如下：

struct Node{
  Node *a[26];
	bool flag;//标志当前单词已完成储存
};
class Trie {
public:
	Node* root;
	Trie() {
		root = new Node();
	}

	void insert(string word) {
		Node* p = root;
		for(int i=0;i<word.length();++i){
			if(p->a[word[i]-97]==NULL){
				p->a[word[i]-97] = new Node();
			}
			p = p->a[word[i]-97];
		}
		p->flag = true;
	}

	bool search(string word) {
		Node* p = root;
		for(int i=0;i<word.length() && p!=NULL;++i){
			if(p->a[word[i]-97]==NULL){
				return false;
			}
			p = p->a[word[i]-97];
		}
		return p->flag;
	}

	bool startsWith(string prefix) {//寻找是否有前缀存在
		Node* p = root;
		for(int i=0;i<prefix.length() && p!=NULL;++i){
			if(!p->a[prefix[i]-97]){
				return false;
			}
			p = p->a[prefix[i]-97];
		}
		return true;
	}
};

2023.3.18

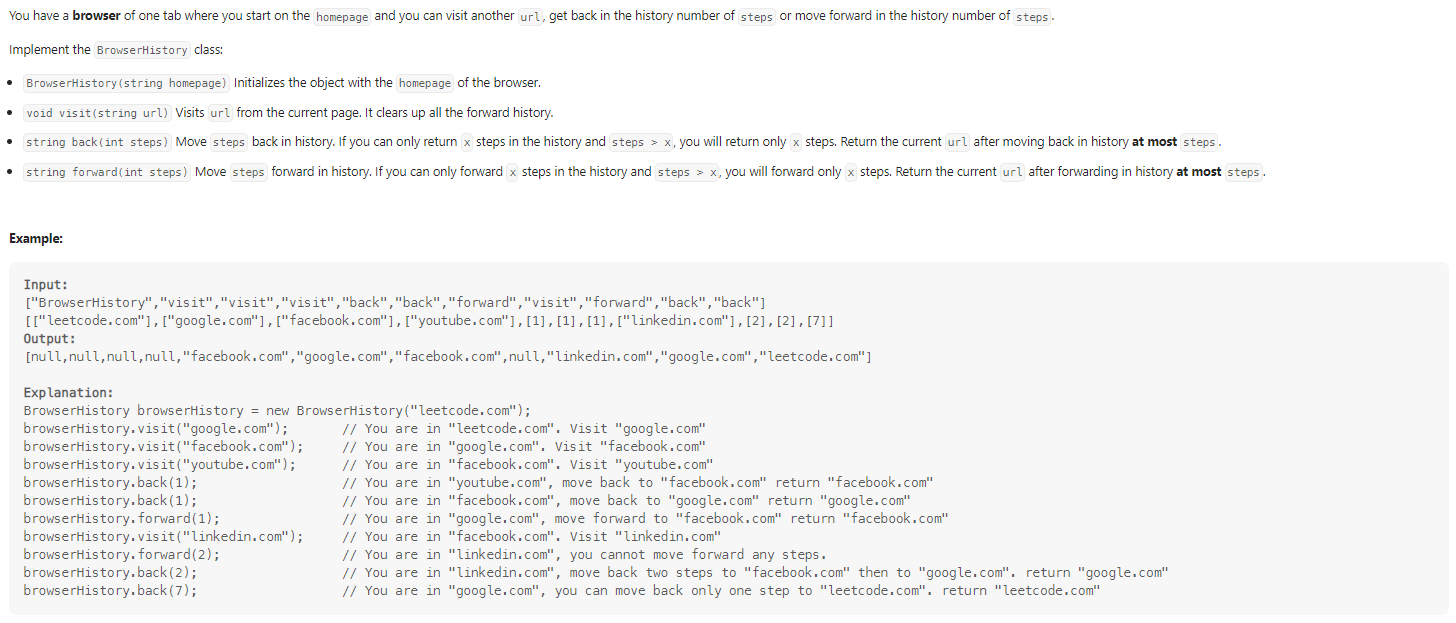
Design Browser History

数据范围：

我的思路：

简单来说就是模拟浏览器的浏览过程，前后访问，之前还考虑复杂了，url数组直接resize就行。

class BrowserHistory {
public:
    vector<string> res;
    int index;
    BrowserHistory(string homepage) {
        res.push_back(homepage);
        index = 0;
    }
    
    void visit(string url) {
        res.resize(index+1);
        res.push_back(url);
        index++;
    }
    
    string back(int steps) {
        index = max(0,index-steps);
        return res[index];
    }
    
    string forward(int steps) {
        int n = res.size() - 1;
        index = min(n , index+steps);
        return res[index];
    }
};

/**
 * Your BrowserHistory object will be instantiated and called as such:
 * BrowserHistory* obj = new BrowserHistory(homepage);
 * obj->visit(url);
 * string param_2 = obj->back(steps);
 * string param_3 = obj->forward(steps);
 */

2023.3.19

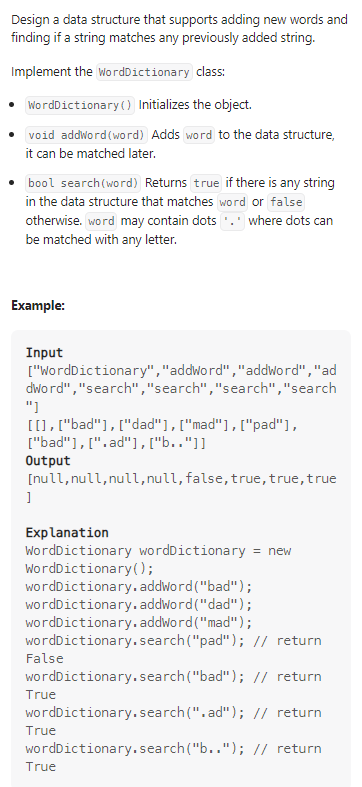
Design Add and Search Words Data Structure

数据范围：

我的思路：

首先是暴力模拟，利用类似散列的方法解决，构建二维数组，其中第一维代表存储单词的长度，将相同长度的单词存储在一个维度中，方便查找。这个方法的时间复杂度和空间复杂度都很低。然后是第二种方法，即利用前缀树完成搜索。两种代码如下：

class WordDictionary {
public:
    vector<vector<string>> res;

    WordDictionary() {
        res.resize(26);        
    }
    
    void addWord(string word) {
        int n = word.length();
        res[n].push_back(word);
    }
    
    bool search(string word) {
        int n = word.length();
        int i,j,flag;
        int nn = res[n].size();
        for(i = 0 ; i < nn ; i++){
            flag = 1;
            for(j = 0 ; j < n ; j++){
                if(word[j]=='.'){
                    continue;
                }
                if(word[j] != res[n][i][j]){
                    flag = 0;
                    break;
                }
            }
            if(flag){
                return true;
            }
        }
        return false;
        
    }
};

class WordDictionary {
public:
    vector<WordDictionary*> root;
    bool end; 

    WordDictionary() {
        root = vector<WordDictionary*>(26,NULL);        
        end = false;
    }
    
    void addWord(string word) {
        WordDictionary *curr = this;
        for(char c : word){
            if(curr->root[c-'a'] == NULL){
                curr->root[c-'a'] = new WordDictionary();
            }
            curr = curr->root[c-'a'];
        }
        curr->end = true;
    }
    
    bool search(string word) {
        WordDictionary *curr = this;
        for(int i = 0 ; i < word.length() ; i++){
            char c = word[i];
            if(c == '.'){
                for(auto ch : curr->root){
                    if(ch && ch->search(word.substr(i+1))){
                        return true;
                    }
                }
                return false;
            }
            if(curr->root[c-'a'] == NULL){
                return false;
            }
            curr = curr->root[c-'a'];
        }
        return curr && curr->end;
    }
}

2023.3.20

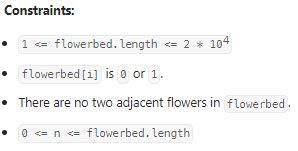
Can Place Flowers

间隔种花，判断种多少：

数据范围：

我的思路：

首先对两个边界进行处理，然后对内部的数据进行穿插处理，得到最后的结果。

class Solution {
public:
    // bool mid_find(vector<int>& flowerbed , int left , int right , int n){
    //     if(n == 0){
    //         return true;
    //     }
    //     while(left<=right){
    //         int mid = left + (right-left)/2;
    //         if(flowerbed)
    //     }
    // }
    bool canPlaceFlowers(vector<int>& flowerbed, int n) {
       int len = flowerbed.size();
       int i;
       int res = n;
       if(len == 1){
            if(n == 0){
                return true;
            }
            else if(n == 1){
                return flowerbed[0] == 1 ? false : true;
            }
        } 
        if(flowerbed[0] == 0 && flowerbed[1] == 0){
            res--;
            flowerbed[0] = 1;
        }
        if(floerbed[len-1] == 0 && flowerbed[len-2] == 0){
            res--;
            flowerbed[len-1] = 1;
        }
        if(n > 2){
            for(i = 1 ; i < n-1 ; i++){
                if(flowerbed[i] == 0 && flowerbed[i-1] == 0 && flowerbed[i+1] == 0){
                    res--;
                    flowerbed[i] = 1;
                }
            }
        }
        if(res <= 0){
            return true;
        }
        return false;
    }
};

2023.3.21

Number of Zero-Filled Subarrays

数据范围：

我的思路：

找到0，标左值，右遍历，找边界，套公式。

class Solution {
public:
    long long mul(long long a,long long b){
        if(b == 0){
            return 1;
        }
        if(b%2 == 0){
            return mul(a,b/2)*mul(a,b/2);
        }
        return a*mul(a,b/2)*mul(a,b/2);
    }
    long long zeroFilledSubarray(vector<int>& nums) {
        long long res = 0;
        long long len;
        int n = nums.size();
        int i = 0,left = 0,right = 0;
        while(i<n){
            if(nums[i] == 0){
                left = i;
                while(i < n - 1 && nums[i] == nums[i+1]){
                    i++;
                }
                len = i - left + 1;
                res = res + len*(1+len)/2;
            }
            i++;
        }
        return res;
    }
};

2023.3.22

Minimum Score of a Path Between Two Cities

数据范围：

我的思路：

主要就是对整个图进行遍历，保存所有能联通的点，然后找到这些点连接边的最小值，代码如下：

class Solution {
public:
    unordered_map<int, vector<int>> r;
    set<int> point;
    void dfs(int index){
        if(point.find(index) != point.end()){
            return ;
        }
        point.insert(index);
        for(auto rr : r[index]){
            dfs(rr);
        }
    }
    int minScore(int n, vector<vector<int>>& roads) {
        for(auto road : roads){
            r[road[0]].push_back(road[1]);
            r[road[1]].push_back(road[0]);
        }
        dfs(1);
        int ans = INT_MAX;
        for(auto road : roads){
            if(point.find(road[0]) != point.end()){
                ans = min(ans,road[2]);
            }
        }
        return ans;
    }
};

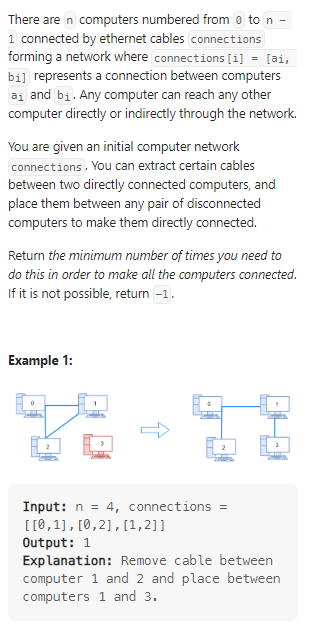
Number of Operations to Make Network Connected

数据范围：

我的思路：

找到所有的连通分量，然后数量减1.这里开始做的时候没有考虑使用并查集。代码如下：

class Solution {
public:
    int makeConnected(int n, vector<vector<int>>& connections) {
        // if there are not enough cables to connect all computers, return -1
        if (connections.size() < n - 1) {
            return -1;
        }
        
        // initialize parent array for Union-Find algorithm
        vector<int> parent(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        
        // union connected computers
        for (auto connection : connections) {
            int parent1 = findParent(parent, connection[0]);
            int parent2 = findParent(parent, connection[1]);
            if (parent1 != parent2) {
                parent[parent1] = parent2;
            }
        }
        
        // count the number of disjoint sets (connected components)
        int numSets = 0;
        for (int i = 0; i < n; i++) {
            if (parent[i] == i) {
                numSets++;
            }
        }
        
        // the number of cables needed is equal to the number of disjoint sets minus 1
        return numSets - 1;
    }
    
    // find the parent of the given node in the Union-Find algorithm
    int findParent(vector<int>& parent, int node) {
        if (parent[node] != node) {
            parent[node] = findParent(parent, parent[node]);
        }
        return parent[node];
    }
};

2023.3.24

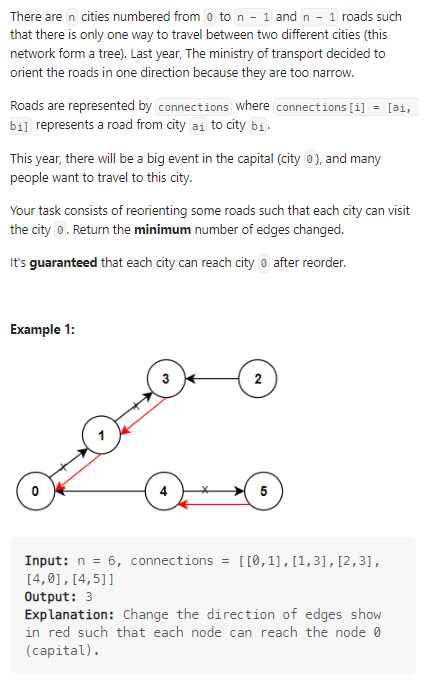
Reorder Routes to Make All Paths Lead to the City Zero

数据范围：

我的思路：

首先是考虑并查集，但是发现简单的并查集情况太多，遂放弃（典）。后来发现层次遍历就够了，如果是正常经过的点，那么必须增加一条新的路径。如果是反向路径才能到达的点，只需要略过即可。

class Solution {
public:
    int minReorder(int n, vector<vector<int>>& connections) {
        queue<int> q;
        int ans = 0;
        int i , nn = connections.size();
        vector<vector<int>> front_(n);
        vector<vector<int>> back(n);
        vector<bool> visit(n,false);
        for(auto connection : connections){
            front_[connection[0]].push_back(connection[1]);
            back[connection[1]].push_back(connection[0]);
        }
        q.push(0);
        while(!q.empty()){
            int temp = q.front();
            visit[temp] = true;
            q.pop();
            for(auto f : front_[temp]){
                if(!visit[f]){
                    ans++;
                    q.push(f);
                }
            }
            for(auto b : back[temp]){
                if(!visit[b]){
                    q.push(b);
                }
            }   
        }
        return ans;
    }
};

2023.3.25

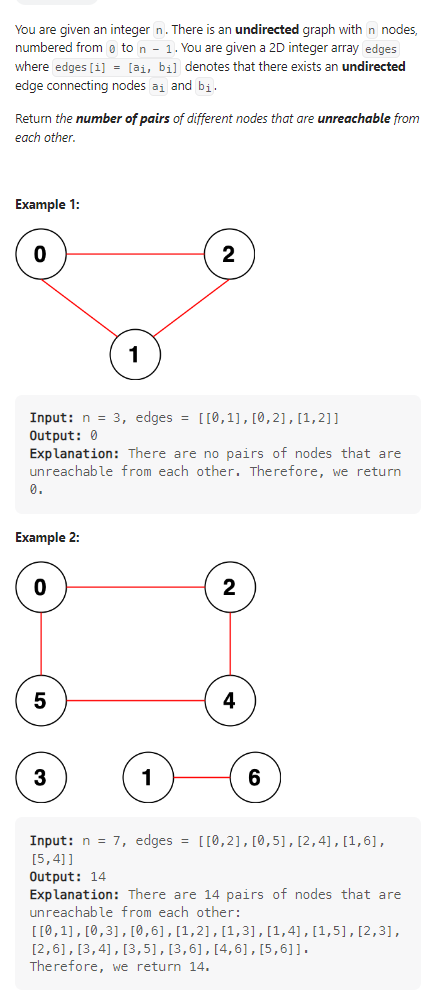
Count Unreachable Pairs of Nodes in an Undirected Graph

数据范围：

我的思路：

第一眼，找到所有的连通分量，然后两两点数量相乘，超时了；换成dfs，对数组进行遍历，找出所有连通分量，两两相乘，超时；用完全图边数去减没每个连通分量的完全图，超时；最后引入unordered_map，问题解决；

class Solution {
public:
    typedef long long ll;
    void dfs(int node, unordered_map<int,vector<int>>& m, ll& cnt, vector<int>& vis){
        vis[node] = 1;
        cnt++;
        for(auto& i: m[node]){
            if(vis[i]==0) dfs(i,m,cnt,vis);   
        }
    }
    long long countPairs(int n, vector<vector<int>>& edges) {
        unordered_map<int,vector<int>> m; // making adjacency list
        for(int i=0;i<edges.size();i++){
            m[edges[i][0]].push_back(edges[i][1]);
            m[edges[i][1]].push_back(edges[i][0]);
        }
        ll ans = ((ll)n*(n-1))/2;
        vector<int> vis(n,0);
        for(int i=0;i<n;i++){
            if(vis[i]==0){ // as node is not visited, we find the no. of nodes in current component.
                ll cnt = 0;
                dfs(i,m,cnt,vis);
                ans -= (cnt*(cnt-1))/2;
            }
        }
        return ans;
    }
};

2023.3.26

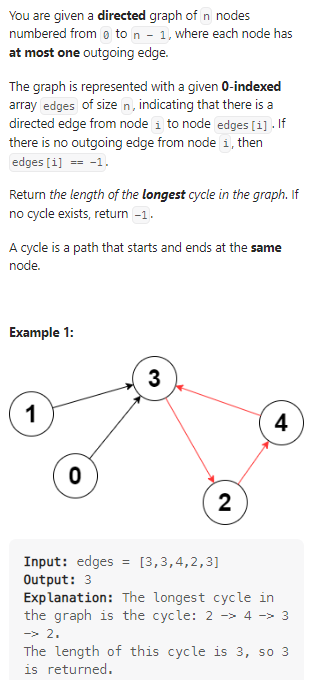
Longest Cycle in a Graph

在有向图中寻找最长的环：

数据范围：

我的思路：

对整个图进行dfs搜索，每次找到可以经过的点，存储相关信息：

• 标记起点的坐标；
• 记录路径的长度；
• 标记当前地址；
• 记录当前小段路径的起始和终端；

当出现无边的情况时，分析是否有环；

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int n = edges.size();
        int i;
        int maxn = -1;
        vector<int> temp(n,0);
        vector<bool> v(n,false);
        vector<int> path(n,0);
        for(i = 0 ; i < n ; i++){
            if(!v[i]){
                int ct = 1;
                int j = -1;
                int k = i;
                while(edges[k]!=-1 && !v[k]){
                    path[k] = i+1;
                    temp[k] = ct;
                    ct++;
                    v[k] = true;
                    j = k;
                    k = edges[k];
                }
                if(edges[k]!=-1){
                    if(path[k] == path[j]){
                        int y =abs(temp[j] - temp[k])+1;
                        maxn = max(maxn,y);
                    }
                }
            }
        }
        return maxn;
    }
};

2023.3.27

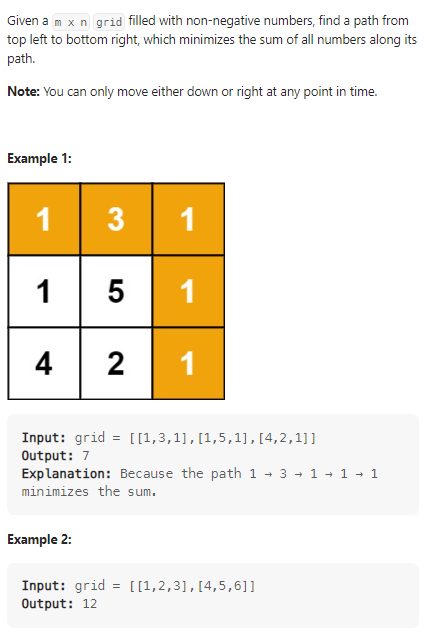
Minimum Path Sum

计算从矩阵左上角到矩阵右下角的最短路径：

数据范围：

我的思路：

首先就是暴力dfs，发现不行只好dp恩算：

class Solution {
public:
    // vector<vector<int>> a;
    // int sum;
    // int m,n;
    // void dfs(int x, int y, int temp){
    //     temp = temp + a[x][y];
    //     if(x == m-1 && y == n-1){
    //         sum = min(temp,sum);
    //         return ;
    //     }
    //     if(x+1 >= 0 && x+1 <= m-1){
    //         dfs(x+1,y,temp);
    //     }
    //     if(y+1 >= 0 && y+1 <= n-1){
    //         dfs(x,y+1,temp);
    //     }
    // }
    int minPathSum(vector<vector<int>>& grid) {
        // a = grid;
        // sum = INT_MAX;
        int m = grid.size();
        int n = grid[0].size();
        // dfs(0,0,0);
        // return sum;

        vector<vector<int>>d(m,vector<int>(n,0));
        int i,j;
        d[0][0] = grid[0][0];
        for(i = 1 ; i < n ;i++){
            d[0][i] = d[0][i-1] + grid[0][i];
        }
        for(i = 1 ; i < m ; i++){
            d[i][0] = d[i-1][0] + grid[i][0];
        }
        for(i = 1 ; i < m ; i++){
            for(j = 1 ; j < n ;j++){
                d[i][j] = min(d[i-1][j],d[i][j-1]) + grid[i][j];
            }
        }
        return d[m-1][n-1];
    }
};

2023.3.28

Minimum Cost For Tickets

数据范围：

我的思路：

明显是一个动态规划问题，需要注意的事递归方式会出现超时问题。需要计算的价值即前一天、前七天和前三十天的价值构成，选择最小值，依次遍历即可，最终得到复杂度为O(N)的算法：

class Solution {
public:
    int mincostTickets(vector<int>& days, vector<int>& costs) {
        set<int> s(days.begin(),days.end());
        int i;
        vector<int> d(366,0);
        for(i = 1 ; i < 366 ; i++){
            d[i] = d[i-1];
            if(s.find(i)!=s.end()){
                d[i] = min(min(d[i-1] + costs[0],d[max(0,i-7)] + costs[1]) , d[max(0,i-30)] + costs[2]);
            }
        }
        return d[365];
    }
};

2023.3.29

Reducing Dishes

在保证菜品的满意度为正值的情况下，尽量提高餐品的数量：

数据范围：

我的思路：

第一眼没看懂题意，以为是只需要关注价值最大即可，后来发现只需要关心菜品数量最大即可；

class Solution {
public:
    static bool cmp(int a, int b){
        return a > b;
    }
    int maxSatisfaction(vector<int>& satisfaction) {
        sort(satisfaction.begin(), satisfaction.end() , cmp);
        int i;
        int n = satisfaction.size();
        int temp = 0;
        int sum = 0;
        for(i = 0 ; i < n ; i++){
            temp += satisfaction[i];
            if(temp < 0){
                break;
            }
            sum += temp;
        }
        return sum;
    }
};

2023.3.30

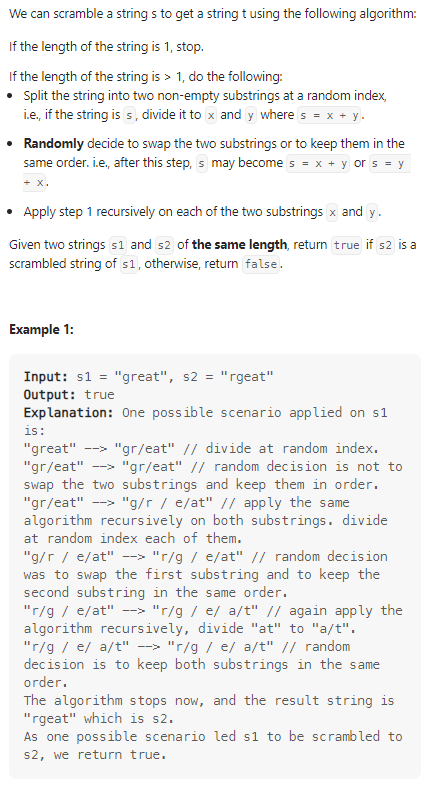
Scramble String

判断s2是否为s1经过变换得到的字符串；

数据范围：

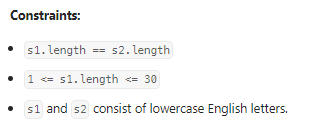
我的思路：

首先想到的就是递归，虽然字符串进行了多次变换，但是对于每一次分隔得到的xy而言，含有的字母和s2中的xy是相同的，通过这个性质我们遍历s1和s2中的所有可能得xy，最终找到最优解：

class Solution {
public:
    unordered_map<string , bool> mp;
    bool isScramble(string s1, string s2) {
        int n = s1.length();
        if(s1.length()!=s2.length()){
            return false;
        }
        if(s1 == s2){
            return true;
        }
        if(n == 1){
            return false;
        }
        string temp = s1 + " " + s2;
        if(mp.find(temp) != mp.end()){
            return mp[temp];
        }
        for(int i = 1 ; i < n ; i++){
            bool ans = (isScramble(s1.substr(0,i),s2.substr(0,i)) && isScramble(s1.substr(i),s2.substr(i)));
            if(ans){
                return true;
            }
            ans = (isScramble(s1.substr(0,i) , s2.substr(n-i)) && isScramble(s1.substr(i) , s2.substr(0,n-i)));
            if(ans){
                return true;
            }
        }
        return mp[temp] = false;
    }
};

2023.3.31

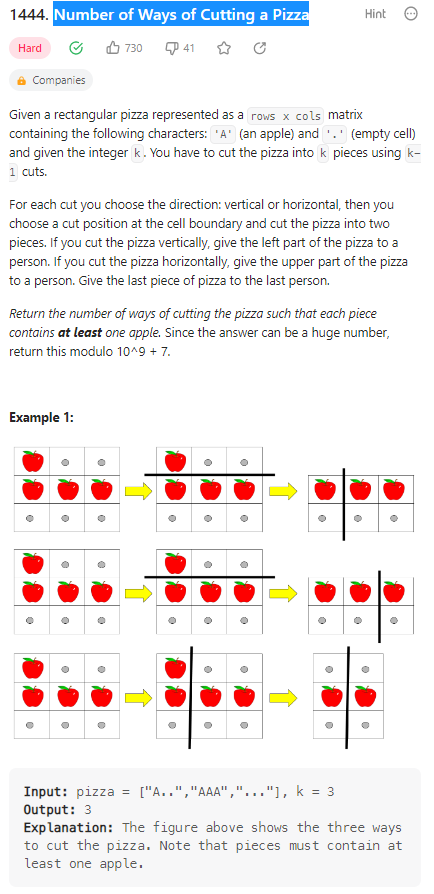
Number of Ways of Cutting a Pizza

分披萨问题，使用k-1次切割分割出k个披萨块，保证每个披萨块上有苹果存在。

数据范围：

我的思路：

很显然是抄的题解，但是具体怎么做呢，我的理解是这样的：

• 首先构建apple矩阵，apple(i,j)存储着右下角含有的所有苹果数量；
• 然后构建dp数组，存储右下角含有苹果的节点；
• 对各行进行遍历，对于apple矩阵相减不为0的结果进行切割（这里就能说明在二者之间切割就一定会有苹果的分离），然后对列进行遍历，重复上述操作；

class Solution {
public:
    int ways(vector<string>& pizza, int k) {
        int rows = pizza.size(), cols = pizza[0].size();
        vector apples(rows + 1, vector<int>(cols + 1));
        vector dp(k, vector(rows, vector<int>(cols)));
        for (int row = rows - 1; row >= 0; row--) {
            for (int col = cols - 1; col >= 0; col--) {
                apples[row][col] = (pizza[row][col] == 'A') + apples[row + 1][col] +
                                   apples[row][col + 1] - apples[row + 1][col + 1];//存储当前坐标的右下角区域所有的苹果数量
                dp[0][row][col] = apples[row][col] > 0;
            }
        }
        const int mod = 1000000007;
        for (int remain = 1; remain < k; remain++) {
            for (int row = 0; row < rows; row++) {
                for (int col = 0; col < cols; col++) {
                    for (int next_row = row + 1; next_row < rows; next_row++) {
                        if (apples[row][col] - apples[next_row][col] > 0) {
                            (dp[remain][row][col] += dp[remain - 1][next_row][col]) %= mod;
                        }
                    }
                    for (int next_col = col + 1; next_col < cols; next_col++) {
                        if (apples[row][col] - apples[row][next_col] > 0) {
                            (dp[remain][row][col] += dp[remain - 1][row][next_col]) %= mod;
                        }
                    }
                }
            }
        }
        return dp[k - 1][0][0];
    }
};