每日一题整理——2023.4

2023.4.1

Binary Search

二分查找，我老想当二分查找的狗了，但是二分查找说她喜欢的是sort

数据范围：

我的思路：

直接上代码，注意搜索空间的控制就好：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        if(n == 1){
            return nums[0] == target ? 0 : -1;
        }
        int left = 0;
        int right = n;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return mid;
            }
            else if(nums[mid] > target){
                right = mid;
            }
            else if(nums[mid] < target){
                left = mid + 1;
            }
        }
        if(nums[left]!=target){
            return -1;
        }
        return left;
    }
};

2023.4.2

Successful Pairs of Spells and Potions

数据范围：

我的思路：

首先想到的就是排序后二分搜索得到最优值，实际的计算结果也是如此：

class Solution {
public:
    vector<int> successfulPairs(vector<int>& spells, vector<int>& potions, long long success) {
        sort(potions.begin() , potions.end());
        int i , j;
        int m = spells.size();
        int n = potions.size();
        vector<int> ans;
        for(int i = 0 ; i < m ; i++){
            long long mid = success/spells[i] + (success%spells[i] ? 1 : 0);
            int left = 0;
            int right = n-1;
            int mid_index;
            while(left <= right){
                mid_index = left + (right - left)/2;
                if(potions[mid_index] < mid){
                    left = mid_index + 1;
                }
                else if(potions[mid_index] >= mid){
                    right = mid_index - 1;
                }
            }
            int index;
            if(potions[mid_index] < mid){
                index = mid_index + 1;
            }
            else{
                index = mid_index;
            }
            ans.push_back(potions.size() - index);
        }
        return ans;
        // for(i = 0 ; i < m ; i++){
        //     long long mid = success/spells[i] + (success % spells[i] ? 1 : 0);
        //     int s = 0 , e = potions.size() - 1 , index , temp;
        //     while(s <= e){
        //         temp = (s + e)/2;
        //         potions[temp] < mid ? s = temp + 1 : e = temp-1; 
        //     }
        //     index = potions[temp] < mid ? temp +1 : temp;
        //     ans.push_back(potions.size() - index);
        // }
        // return ans;
    }
};

2023.4.3

Boats to Save People

无限船制，每一艘船只能搭载两个人，这两个人的重量不能超过limit，问最小船数。

数据范围：

我的思路：

之前想复杂了，以为每一艘船不止能搭载两个人，后来发现用贪心算一下就好了。

class Solution {
public:
    int numRescueBoats(vector<int>& people, int limit) {
        sort(people.begin() , people.end());
        int n = people.size();
        int left = 0;
        int right = n-1;
        while(left < right){
            if(people[left] + people[right] <= limit){
                left++;
            }
            right--;
        }
        return n-left;
    }
};

2023.4.4

Optimal Partition of String

数据范围：

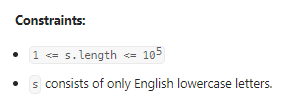
我的思路：

这题迷惑性比较大，虽然条条框框很多，其实只要对其进行遍历，每次找到出现过的元素就进行一次切割，得到的就是最少的分段。

class Solution {
public:
    int partitionString(string s) {
        vector<int> last(26,-1);
        int count = 1 ;
        int index = 0;
        for(int i = 0 ; i < s.length() ; i++){
            if(last[s[i]-'a'] >= index){
                count++;
                index = i;
            }
            last[s[i]-'a'] = i;
        }
        return count;
    }
};

2023.4.6

Number of Closed Islands

找出所有的空岛，空岛为上下左右都是水的连通集：

数据范围：

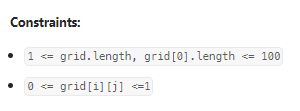
我的思路：

首先对边界进行处理，排除掉所有边界上的陆地对内部的影响，然后对内部进行深度搜索，每计算一次进行一次计数，最终得到结果。

class Solution {
public:
    const int d1[4] = {0,1,0,-1};
    const int d2[4] = {1,0,-1,0};
    int m,n;
    void dfs(int x, int y,vector<vector<int>>& grid){
        grid[x][y] = 1;
        for(int i = 0 ; i < 4 ; i++){
            int xx = x + d1[i];
            int yy = y + d2[i];
            if(xx>=0 && xx<m && yy>=0 && yy<n && grid[xx][yy] == 0){
                dfs(xx,yy,grid);
            }
        }
    }
    int closedIsland(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int i,j;
        int ans = 0;
        for(i = 0 ; i < m ; i++){
            if(grid[i][0] == 0)
                dfs(i,0,grid);
            if(grid[i][n-1] == 0)
                dfs(i,n-1,grid);
        }
        for(j = 0 ; j < n ; j++){
            if(grid[0][j] == 0)
                dfs(0,j,grid);
            if(grid[m-1][j] == 0)
                dfs(m-1,j,grid);
        }
        for(i = 1 ; i < m-1 ; i++){
            for(j = 1 ; j < n-1 ; j++){
                if(grid[i][j] == 0){
                    ans++;
                    dfs(i,j,grid);
                }
            }
        }
        return ans;
    }
};

2023.4.7

Number of Enclaves

数据范围：

我的思路：

跟昨天的题差不多，对边界进行处理之后查询内部的陆地个数即可；

代码如下：

class Solution {
public:
    const int d[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
    int m,n;
    void dfs(int x, int y, vector<vector<int>>& grid){
        if(grid[x][y] == 0){
            return;
        }
        grid[x][y] = 0;
        for(int i = 0 ; i < 4 ; i++){
            int xx = x + d[i][0];
            int yy = y + d[i][1];
            if(xx >= 0 && yy >= 0 && xx < m && yy < n){
                dfs(xx,yy,grid);
            }
        }
    }
    int numEnclaves(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int i,j;
        for(i = 0 ; i < m ; i++){
            dfs(i,0,grid);
            dfs(i,n-1,grid);
        }
        for(i = 0 ; i < n ; i++){
            dfs(0,i,grid);
            dfs(m-1,i,grid);
        }
        int count = 0;
        for(i = 1 ; i < m-1 ; i++){
            for(j = 1 ; j < n-1 ; j++){
                if(grid[i][j] == 1){
                    count++;
                }
            }
        }
        return count;
    }
};

2023.4.8

Clone Graph

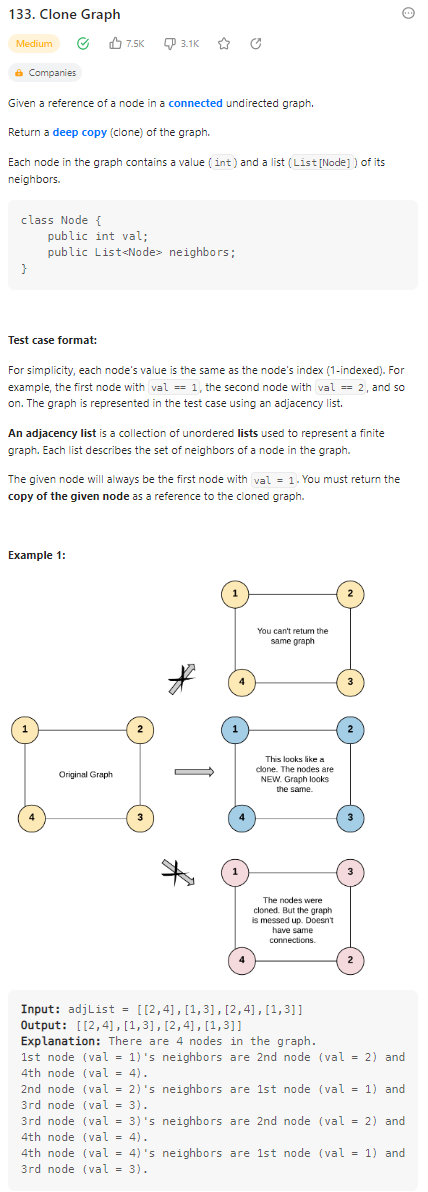
数据范围：

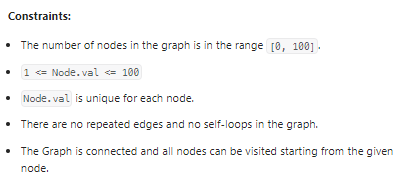
我的思路：

整体过程很简单，dfs直搜即可，但是需要注意新增neighbor节点时需要考虑不要设重了。代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;
    Node() {
        val = 0;
        neighbors = vector<Node*>();
    }
    Node(int _val) {
        val = _val;
        neighbors = vector<Node*>();
    }
    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/

class Solution {
public:
    Node* dfs(Node* cur , unordered_map<Node* , Node*> &mp){
        vector<Node*> neighbor;
        Node* clone = new Node(cur->val);
        mp[cur] = clone;
        for(auto it : cur->neighbors){
            if(mp.find(it)!=mp.end()){
                neighbor.push_back(mp[it]);
            }
            else{
                neighbor.push_back(dfs(it,mp));
            }
        }
        clone->neighbors = neighbor;
        return clone;
    }
    Node* cloneGraph(Node* node) {
        unordered_map<Node*,Node*> mp;
        if(node == NULL){
            return NULL;
        }
        if(node->neighbors.size() == 0){
            Node* clone = new Node(node->val);
            return clone;
        }
        return dfs(node,mp);
    }
};

2023.4.10

Valid Parentheses

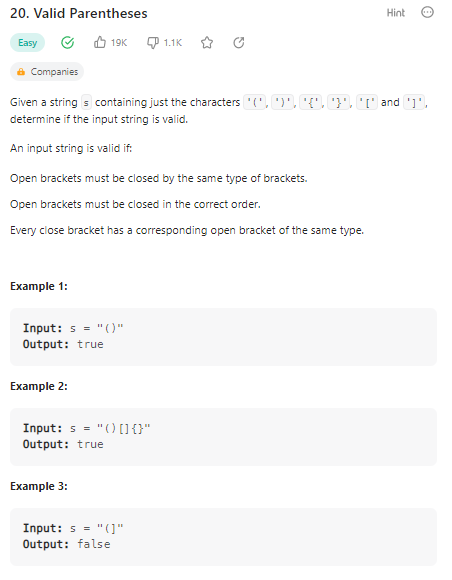
数据范围：

我的思路：

入栈，根据符号优先级进行筛选，代码如下：

class Solution {
public:
    bool isValid(string s) {
        map<char,int> mp;
        mp['('] = 1;
        mp[')'] = 1;
        mp['{'] = 2;
        mp['}'] = 2;
        mp['['] = 3;
        mp[']'] = 3;
        stack<char> ss;
        int n = s.length();
        for(int i = 0 ; i < n ; i++){
            if(s[i] == '(' || s[i] == '{' || s[i] == '['){
                ss.push(s[i]);
            }
            else{
                if(ss.empty()){
                    return false;
                }
                char temp = ss.top();
                if(mp[temp] == mp[s[i]]){
                    ss.pop();
                }
                else{
                    return false;
                }
            }
        }
        if(ss.empty()){
            return true;
        }
        return false;;
    }
};

2023.4.11

Removing Stars From a String

数据范围：

我的思路：

整体上看是移除所有*相关的字符串，注意一些提高速度的技巧即可。

class Solution {
public:
    string removeStars(string s) {
        stack<char> ss;
        int len = s.length();
        int index = 0;
        int count_1 = 0;
        string result;
        while(index < len){
            if(s[index] == '*'){
                if(ss.empty()){
                    count_1++;
                }
                else{
                    ss.pop();
                }
            }
            else{
                if(count_1 > 0){
                    count_1--;
                }
                else{
                    ss.push(s[index]);
                }
            }
            index++;
        }
        while(!ss.empty()){
            result += ss.top();
            ss.pop();
        }
        reverse(result.begin() , result.end());
        return result;
    }
};

2023.4.12

Simplify Path

数据范围：

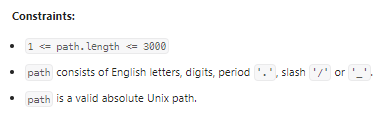
我的思路：

文件系统的模拟，用栈保存每个路径上文件的名称，注意.对文件结构的影响。

class Solution {
public:
    string simplifyPath(string path) {
        stack<string> s;
        string result;
        int i = 0, n = path.length();
        while(i < n){
            if(path[i] == '/'){
                i++;
                continue;
            }
            string temp;
            while(i < n && path[i] != '/'){
                temp += path[i];
                i++;
            }
            if(temp == "."){
                continue;
            }   
            else if(temp == ".."){
                if(!s.empty()){
                    s.pop();
                } 
            }
            else{
                s.push(temp);
            }
        }
        while(!s.empty()){
            result = "/" + s.top() + result;
            s.pop();
        }
        if(result == ""){
            result = "/";
        }
        return result;
    }
};

2023.4.13

Validate Stack Sequences

数据约束：

我的思路：

这道题的解法就是构造一个真实的栈，对栈持续进行弹进弹出操作，需要注意的是当元素和栈顶不相同时的处理方法，这里我构造了一个访问数组进行标记。

class Solution {
public:
    bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
        stack<int> s;
        int left = 0;
        int left_1 = 0;
        int m = pushed.size();
        int n = popped.size();
        const int maxn = 1001;
        bool v[maxn] = {false};

        s.push(pushed[left]);
        v[pushed[left++]] = true;
        while(left_1 < n){
            int temp = s.top();
            if(popped[left_1] == temp){
                s.pop();
            }
            else{
                if(!v[popped[left_1]]){
                    while(left < m && s.top()!=popped[left_1]){
                        s.push(pushed[left]);
                        v[pushed[left++]] = true;
                    }
                    if(s.top() == popped[left_1]){
                        s.pop();
                    }
                    else{
                        return false;
                    }
                }
                else if(v[popped[left_1]] && s.top() == popped[left_1]){
                    s.pop();
                }
                else{
                    return false;
                }
            }
            if(s.empty() && left < m){
                s.push(pushed[left++]);
            }
            left_1++;
        }
        return true;
    }
};

2023.4.14

Longest Palindromic Subsequence

寻找字符串中最有可能得回文串；

数据范围：

我的思路：

动态规划，对于可能存在的字符串而言，需要从前往后考虑是否为回文，回文的判断代码整体如下：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<int> dp(n,0);
        for(int i = n-1 ; i >= 0 ; i--){
            vector<int> temp(n,0);
            temp[i] = 1;
            for(int j = i + 1 ; j < n ; j++){
                if(s[i] == s[j]){
                    temp[j] = 2 + dp[j-1];
                }
                else{
                    temp[j] = max(dp[j],temp[j-1]);
                }
            }
            dp = temp;
        } 
        return dp[n-1];
    }
};

2023.4.15

Maximum Value of K Coins From Piles

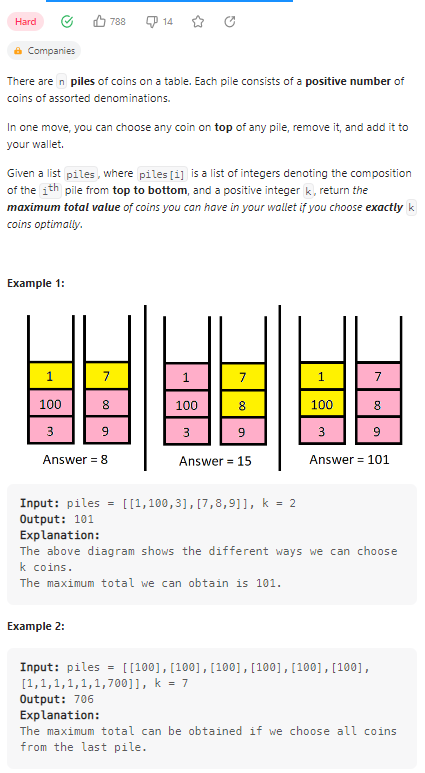
数据范围：

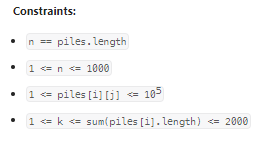
我的思路：

利用动态规划计算，首先构建一个k长度的数组，dp[k]代表取k个硬币时能够得到的最大值。每次遍历都会更新一个堆，piles[i][j]第i个堆取前j个元素后得到的数值。然后对dp数组进行遍历，考虑当前的堆，更新dp的每一个值。具体代码如下：

class Solution {
public:
    int maxValueOfCoins(vector<vector<int>>& piles, int k) {
        int m = piles.size();
        vector<int> dp(k+1,0),pre(k+1,0);
        for(int i = 0 ; i < m ; i++){
            for(int j = 1 ; j < piles[i].size() ; j++){
                piles[i][j] += piles[i][j-1];
            }
            for(int j = 1 ; j <= k ; j++){
                dp[j] = pre[j];
                for(int l = 1 ; l <= min(j,(int)piles[i].size()) ; l++){
                    dp[j] = max(dp[j] , piles[i][l-1]+pre[j-l]);
                }
            }
            pre = dp;
        }
        return dp[k];
    }
};

2023.4.18

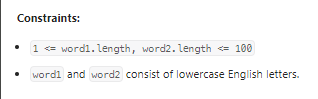
Merge Strings Alternately

交替合并两个字符串。

数据范围：

我的思路：

设立两个指针交替赋值即可。（力扣已经连续两天每日一题摆烂，望周知）

class Solution {
public:
    string mergeAlternately(string word1, string word2) {
        string res = "";
        int index_1 = 0;
        int index_2 = 0;
        int n = word1.length();
        int m = word2.length();
        while(index_1 < n && index_2 < m){
            res += word1[index_1++];
            res += word2[index_2++];
        }
        res += word1.substr(index_1);
        res += word2.substr(index_2);
        return res;
    } 
};

2023.4.19

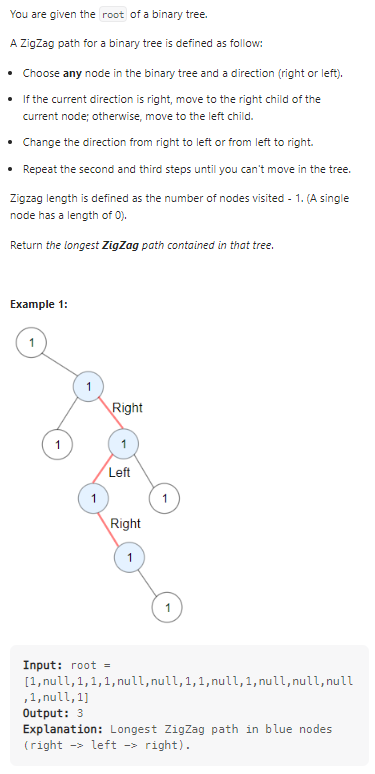
Longest ZigZag Path in a Binary Tree

计算二叉树的zigzag路径：

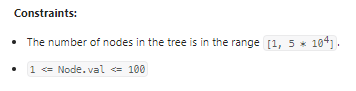
数据范围：

我的思路：

一眼dfs，注意递归的数量，第一遍主函数都自递归了一遍，感觉很蠢。下次注意了。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;
    void now_longest(TreeNode* root, int flag , int len){
        if(root == NULL){
            return ;
        }
        ans = max(ans,len);
        if(flag == 0){
            now_longest(root->right,1,len+1);
            now_longest(root->left,0,1);
        }
        else{
            now_longest(root->left,0,len+1);
            now_longest(root->right,1,1);
        }
    }
    int longestZigZag(TreeNode* root) {
        if(root == NULL){
            return 0;
        }
        now_longest(root->left,0,1);
        now_longest(root->right,1,1);
        return ans;
    }
};

求斐波那契数列F的第n项

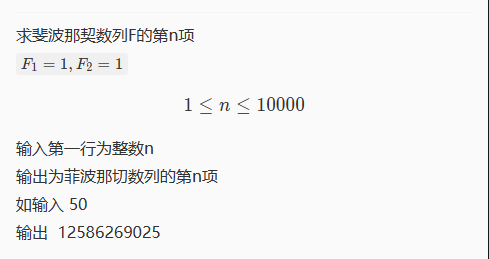
嗨呀，是我最喜欢的模拟吗？感觉写的有点shi，以后再改。

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
typedef long long ll;

const int maxn = 10001;
string a[maxn];

string add(string s1, string s2) {
	int m = s1.length();
	int n = s2.length();
	string res;
	int index_1 = m - 1;
	int index_2 = n - 1;
	int plus = 0;
	while (index_1 >= 0 && index_2 >= 0) {
		int tmp1 = s1[index_1--] - '0';
		int tmp2 = s2[index_2--] - '0';
		int tmp = tmp1 + tmp2 + plus;
		if (tmp < 10) {
			char temp = tmp + '0';
			res += temp;
			plus = 0;
		}
		else {
			plus = 1;
			char temp = tmp - 10 + '0';
			res += temp;
		}
	}
	while (index_1 >= 0) {
		int tmp = s1[index_1--] - '0' + plus;
		if (tmp < 10) {
			plus = 0;
			char temp = tmp + '0';
			res += temp;
		}
		else {
			plus = 1;
			char temp = tmp - 10 + '0';
			res += temp;
		}
	}
	while (index_2 >= 0) {
		int tmp = s2[index_2--] - '0' + plus;
		if (tmp < 10) {
			plus = 0;
			char temp = tmp + '0';
			res += temp;
		}
		else {
			plus = 1;
			char temp = tmp - 10 + '0';
			res += temp;
		}
	}
	if (plus == 1) {
		res += "1";
	}
	reverse(res.begin(), res.end());
	return res;
}

int main() {
	int n;
	scanf("%d", &n);
	a[1] = "1";
	a[2] = "1";
	for (int i = 3; i <= n; i++) {
		a[i] = add(a[i - 1], a[i - 2]);
	}
	cout << a[n] << endl;
	return 0;
}

2023.4.20

Maximum Width of Binary Tree

二叉树的最大宽度；

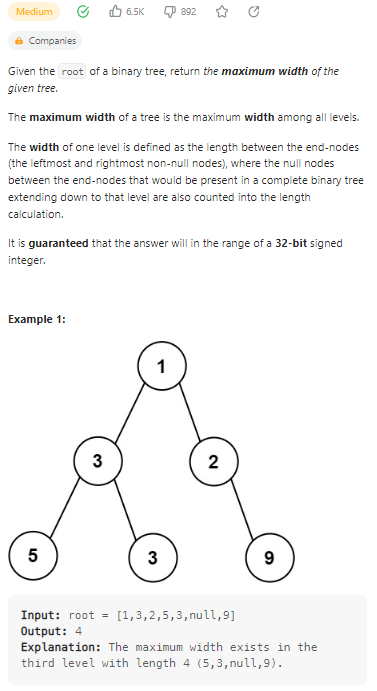
数据范围：

我的思路：

最初想法：层序遍历+新节点添加，发现麻烦了，超时；

后续想法：利用父节点进行计数，然后一减不就好了；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        if(root == NULL){
            return 0;
        }
        int max_len = 1;
        queue<pair<TreeNode* , int>> q;
        q.push({root , 0});

        while(!q.empty()){
            int level_size = q.size();
            int start_index = q.front().second;
            int end_index = q.back().second;
            max_len = max(max_len , end_index - start_index + 1);
            for(int i = 0 ; i < level_size ; i++){
                auto node_index_pair = q.front();
                TreeNode* node = node_index_pair.first;
                int node_index = node_index_pair.second - start_index;
                q.pop();

                if(node->left){
                    q.push({node->left , 2LL * node_index + 1});
                }
                if(node->right){
                    q.push({node->right , 2LL * node_index + 2});
                }
            }
        }
        return max_len;
    }
};

2023.4.21

Profitable Schemes

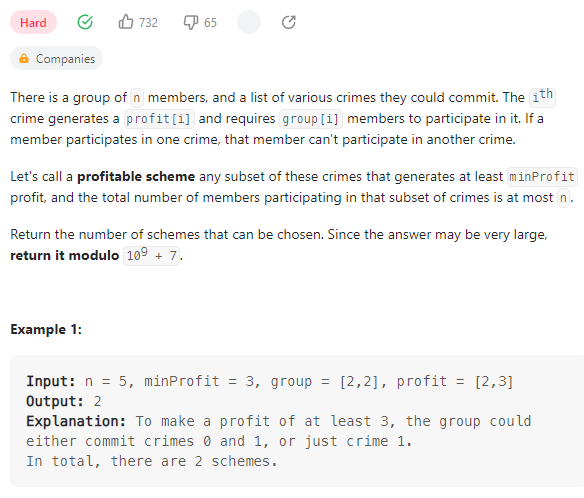
数据范围：

我的思路：

对于n个人，存在最小的利益minProfit，两个长度相同的数组，分别存储某个犯罪事件的参与人数和最大价值，想要知道有多少种方案分配人数使利益至少为minProfit。这里动态变化的事两个量，一个就是组合事件构成的价值，另一个是参与组合事件的人数。因此这里给出dp[i][j]的构造：

$$dp[i][j] = dp[i][j] + dp[i-value_p][j-value_g]$$

其中，dp[i][j]代表组合价值为i、j个人参加时得到的方案数，value_p代表当前实践的价值，value_g代表当前参与组合事件的人数，代码如下：

class Solution {
public:
    const int mod = 1000000007;
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
        int m = group.size();
        vector<vector<int>> dp(minProfit+1 , vector<int>(n+1 , 0));
        dp[0][0] = 1;
        for(int i = 0 ; i < m ; i++){
            int group_value = group[i];
            int profit_value = profit[i];
            for(int j = minProfit ; j >= 0 ; j--){
                for(int k = n-group_value ; k >= 0 ; k--){
                    int temp = min(j+profit_value , minProfit);
                    dp[temp][k+group_value] += dp[j][k];
                    dp[temp][k+group_value] %= mod;
                }
            }
        }
        int sum = 0;
        for(int i = 0 ; i <= n ; i++){
            sum += dp[minProfit][i];
            sum %= mod;
        }
        return sum;
    }
};

2023.4.22

最长等差数列

计算数列内部的最长等差数列，可以不连续；

数据范围：

我的思路：

首先注意到序列是可以不连续的，因此记忆化搜索是必要的。因此使用dp[i][j]表示以nums[i]结束的序列中，公差为j的等差数列的最长长度。因此得到如下的推导式：

$$dp[i][j] = max(dp[i][j] , dp[k][j]+1) \quad (其中j = nums[i]-nums[k]+500)$$

加五百的原因是防止下标的溢出，最后的代码如下：

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) {
        int n = nums.size();
        int ans = 0;
        vector<vector<int>> dp(n,vector<int>(1001,0));
        for(int i = 1 ; i < n ; i++){
            for(int j = 0 ; j < i ; j++){
                int d = nums[i] - nums[j] + 500;
                dp[i][d] = max(dp[i][d] , dp[j][d]+1);
                ans = max(ans,dp[i][d]);
            }
        }
        return ans+1;
    }
};

2023.4.24

Last Stone Weight

数据范围：

我的思路：
利用优先队列实时排序，然后进行层次遍历就可以了。

class Solution {
public:
    int lastStoneWeight(vector<int>& stones) {
        priority_queue<int , vector<int> , less<int>> q;
        int n = stones.size();
        for(int i = 0 ; i < n ; i++){
            q.push(stones[i]);
        }
        while(q.size() > 1){
            int tmp1 = q.top();
            q.pop();
            int tmp2 = q.top();
            q.pop();
            if(tmp1 != tmp2){
                int temp = tmp1 < tmp2 ? (tmp2-tmp1) : (tmp1-tmp2);
                q.push(temp);
            }
        }
        if(q.size() == 0){
            return 0;
        }    
        return q.top();
    }
};

2023.4.24

按字典序排在最后的子串

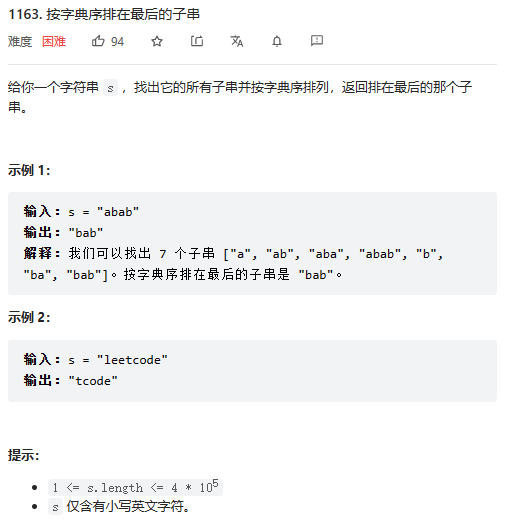
我的思路：

字典序最后一个字符串，毫无疑问的是他的左端是全串最小的，而且他一定是一个后缀串。掌握了这些知识后，只需要双指针计算最长最大后缀串即可。这里需要考虑优化问题，即左端不再遍历已经比对过的点。最后的代码如下：

class Solution {
public:
    string lastSubstring(string s) {
        int k = 0 , i = 0 , j = 1;
        int n = s.size();
        while(j + k < n){
            if(s[i+k] == s[j+k]){//如果两端相同，则都进行跳过操作；
                k++;
            }
            else{
                if(s[i+k] < s[j+k]){//如果左端小于右端，左端推进，找到最大值
                    i = i+k+1;
                }
                else{//如果右端小于左端，继续推进右端，找到最后
                    j = j+k+1;
                }
                if(i == j){
                    j++;
                }
                k = 0;
            }
        }
        return s.substr(i);
    }
};

2023.4.26

Add Digits

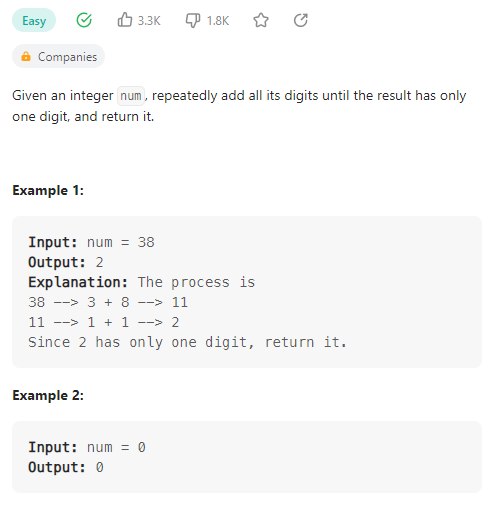
范围：

我的思路：

首先是递归和非递归的模拟，其次就是新的方法：对于任何一个整数x，当他的各位之和等于y时，存在以下的式子：

$$y \quad = x(mod 9)$$

证明比较简单，不再赘述：

class Solution {
public:
    int addDigits(int num) {
        if(num == 0){
            return 0;
        }
        if(num%9 == 0){
            return 9;
        }
        return num%9;
    }
};

两个非重叠子数组的最大和

数据范围：

我的思路：

数据范围较小，因此前缀和+暴力模拟就足够了，之前尝试了dp的做法，发现需要记忆的内容太多了，最后没用滑动窗口都过了，令人感慨。

class Solution {
public:
    int maxSumTwoNoOverlap(vector<int>& nums, int firstLen, int secondLen) {
        int n = nums.size();
        vector<int> first_len(n,0);
        vector<int> second_len(n,0);
        for(int i = 0 ; i < firstLen ; i++){
            first_len[firstLen-1] += nums[i];
        }
        for(int i = 0 ; i < secondLen ; i++){
            second_len[secondLen-1] += nums[i];
        }
        for(int i = firstLen ; i < n ; i++){
            first_len[i] = first_len[i-1]+nums[i]-nums[i-firstLen];
        }
        for(int i = secondLen ; i < n ; i++){
            second_len[i] = second_len[i-1]+nums[i]-nums[i-secondLen];
        }
        int max_first = -1;
        for(int i = 0 ; i < n ; i++){
            for(int j = 0 ; j < n ; j++){
                if(i < (j-secondLen+1) || j < (i-firstLen+1)){
                    max_first = max(first_len[i]+second_len[j] , max_first);
                }
            }
        }
        return max_first;
    }
};

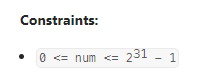
Bulb Switcher

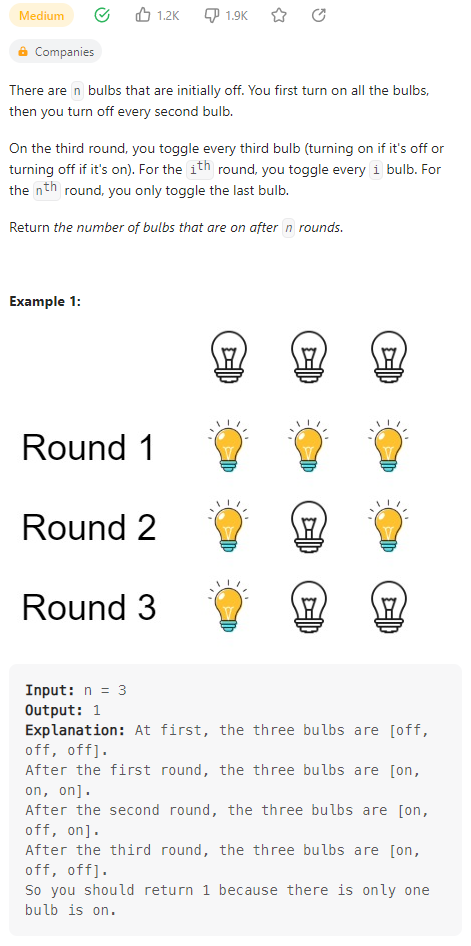
数据范围：

我的思路：

数据范围很大，我还存着侥幸心理试了试暴力+埃氏筛，结果不出所料挂了。看了题解，发现原来这么简单：对于灯泡i而言，只有当他的因子数量为奇数时，才会在最后不被关闭，因此只需要找出所有因子数量是奇数的序号即可。恰好，因子数量是奇数的数字为平方数，因此只需要统计n中的平方数即可；

class Solution {
public:
    int bulbSwitch(int n) {
        return sqrt(n);
    }
};

2023.4.28

Similar String Groups

数据范围：

我的思路：

记录一下，第一次做出来hard题，虽然花了一个小时的时间，基本的思路就是构建并查集，对于同一个集合的字符串进行归类操作。在两个字符串的比较上，我使用双指针的方法逼近最优，感觉如果多练一练就能半个小时写完，最后半个小时完全就是修改小错误、小bug；

class Solution {
public:
    vector<int> father;
    bool check_str(string s1 , string s2){
        if(s1 == s2){
            return true;
        }
        int i = 0;
        int len = s1.length();
        int left = 0;
        int right = len-1;
        while(s1[left] == s2[left]){
            left++;
        }
        while(s1[right] == s2[right]){
            right--;
        }
        swap(s2[left],s2[right]);
        while(left < right){
            if(s1[left]!=s2[left] || s1[right]!=s2[right]){
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
    int find_father(int index){
        if(index == father[index]){
            return index;
        }
        return father[index]=find_father(father[index]);
    }
    void union_set(int x,int y){
        int fx = find_father(x);
        int fy = find_father(y);
        father[fy] = fx;
    }
    int numSimilarGroups(vector<string>& strs) {
        int n = strs.size();
        father.resize(n);
        set<int> ss;
        for(int i = 0 ; i < n ; i++){
            father[i] = i;
        }
        for(int i = 0 ; i < n ; ++i){
            for(int j = i+1 ; j < n ; j++){
                if(check_str(strs[i] , strs[j])){
                    union_set(i,j);
                }
            }
        }
        for(int i = 0 ; i < n ; i++){
            ss.insert(find_father(i));
        }
        return ss.size();
    }
};

2023.4.28

餐盘栈

数据范围：

我的思路：

我擦，连续两道困难题暴力都过了，疑似今天运气很好。整个数据结构中，最小元素为node，代表一个栈，其中包含vector和top。利用size存储最大容量，index存储左端点（即右侧第一个不为空的栈），use_index用于存储第一个存在空余的栈。

对于push操作和pop操作，首先考虑当前状态是否能进行操作，操作完成后考虑两端点的位置是否合法。对于popAtStack操作，需要考虑两端点的合法性，同时注意空栈情况的处理。

struct Node{
    int top;
    vector<int> s;
    Node(){
        top=0;
    }
};
const static int maxn = 200001;
class DinnerPlates {
public:
    Node node[maxn];
    int size;
    int index;
    int use_index;
    DinnerPlates(int capacity) {
        size = capacity;
        index = 0;
        use_index = 0;
    }

    void push(int val) {
        if(node[use_index].top == size){
            while(use_index <= index && node[use_index].top == size){
                use_index++;
            }
            if(use_index > index){
                index++;
            }
        }
        node[use_index].s.push_back(val);
        node[use_index].top++;
    }
    
    int pop() {
        while(index >= 0 && node[index].top == 0){
            index--;
        }
        if(index == -1){
            index = 0;
            use_index = 0;
            return -1;
        }
        if(index < use_index){
            use_index = index;
        }
        int result = node[index].s[node[index].top-1];
        node[index].s.pop_back();
        node[index].top--;
        return result;
    }
    
    int popAtStack(int index_1) {
        if(node[index_1].top == 0){
            return -1;
        }
        int result = node[index_1].s[node[index_1].top-1];
        node[index_1].s.pop_back();
        node[index_1].top--;
        if(index_1 < use_index){
            use_index = index_1;
        }
        if(index_1 == index && node[index_1].top == 0 && index!=0){
            if(use_index == index){
                use_index--;
            }
            index--;
        }
        return result;
    }
};

/**
 * Your DinnerPlates object will be instantiated and called as such:
 * DinnerPlates* obj = new DinnerPlates(capacity);
 * obj->push(val);
 * int param_2 = obj->pop();
 * int param_3 = obj->popAtStack(index);
 */

2023.4.29

Checking Existence of Edge Length Limited Paths

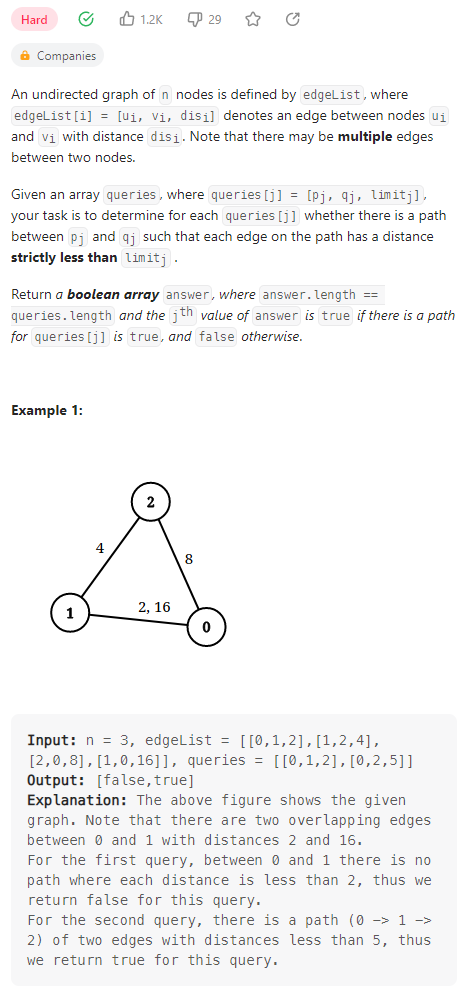
数据范围：

我的思路：

对于每一次的查询，进行地杰斯特拉的最短路搜索，同时存储每个节点最短路径的前驱节点信息，然后对最短路径上各点的边长进行分析，从而确定查询结果。然后自然RE了（甚至是第三个样例的RE了，输完了）

之后看了评论区的做法，感觉我会做的方法有下面这种：首先，根据并查集的思想构建各个节点的father，然后对各个边长和各个查询根据长度从小到大排序，从初始最短查询开始遍历，判断当前边是否超出标准，以此类推。整体上看，算法优化了每次查询都去反复查询最短边的问题，效果较好。

class DSU {
    public:
    vector<int> Parent, Rank;
    DSU(int n) {
        Parent.resize(n);
        Rank.resize(n, 0);
        for (int i = 0; i < n; i++) Parent[i] = i;
    }
    int Find(int x) {
        return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);
    }
    bool Union(int x, int y) {
        int xset = Find(x), yset = Find(y);
        if (xset != yset) {
            Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;
            Rank[xset] += Rank[xset] == Rank[yset];
            return true;
        }
        return false;
    }
};

class Solution {
public:
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
        DSU dsu(n);//构建并查集的父亲数组
        for(int i=0;i<queries.size();i++)
            queries[i].push_back(i);//对于每一次的查询，将对应的序号插入，避免排序的影响
        
        sort(queries.begin(), queries.end(), [&](auto const &a, auto const &b){
            return a[2] < b[2];
        });//根据标准长度，由小到大对询问进行排序
        sort(edgeList.begin(), edgeList.end(), [&](auto const &a, auto const &b){
            return a[2] < b[2];
        });//根据边长，由小到大对各条边进行排序
        
        int i=0;
        vector<bool> res(queries.size(), false);
        for(auto q: queries){
            while(i<edgeList.size() && edgeList[i][2]<q[2]){
                dsu.Union(edgeList[i][0] , edgeList[i][1]);
                i++;
            }
            if(dsu.Find(q[0]) == dsu.Find(q[1]))//如果查询的起点和中点位于同一个集合，说明两点之间存在一条更短的路径联通，因此这条边是可以通过审查的
                res[q[3]] = true;
        }
        
        return res;
    }
};