图神经网络学习

参考文献：https://distill.pub/2021/gnn-intro/

前言

图神经网络的基本结构：

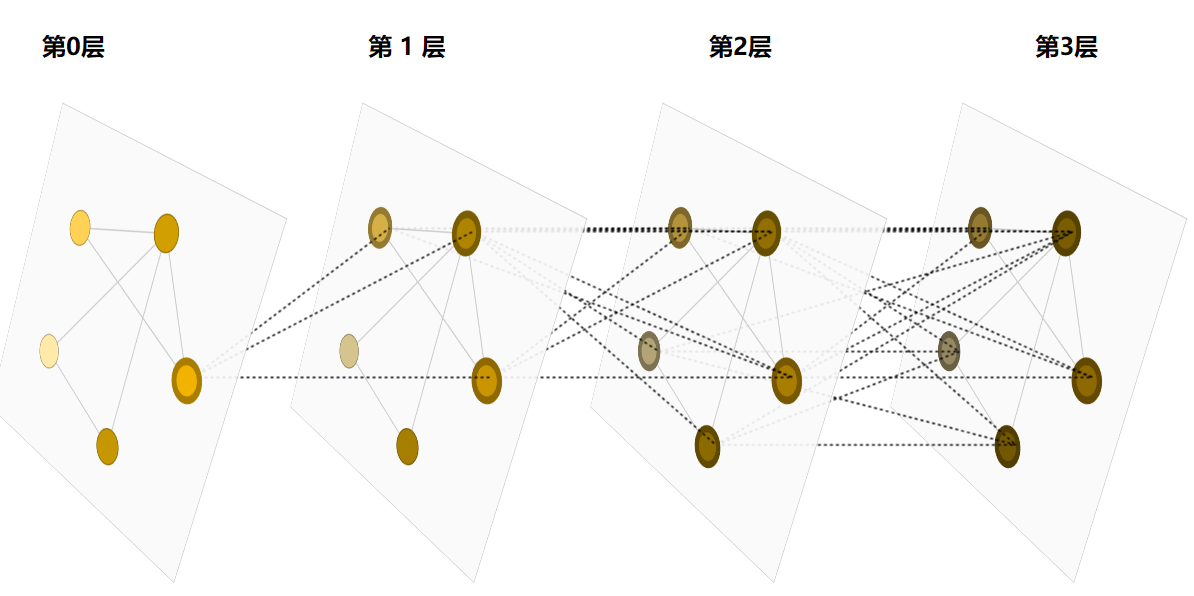
可以看到，在每一层传播之后图的基本结构没有发生变化，只对顶点、边以及全局信息进行了调整，也就是权重的变化。图中给出了节点的信息是如何传递的，可以看出每一层的特定节点输出都是与结构上相邻节点的信息输入有关。

图的定义

理论上，任何数据都可以转化成图的形式，然后在神经网络中进行传播、训练。在图像处理领域，可以根据图像的像素矩阵中各像素块之间的邻接关系构建相关数据结构：

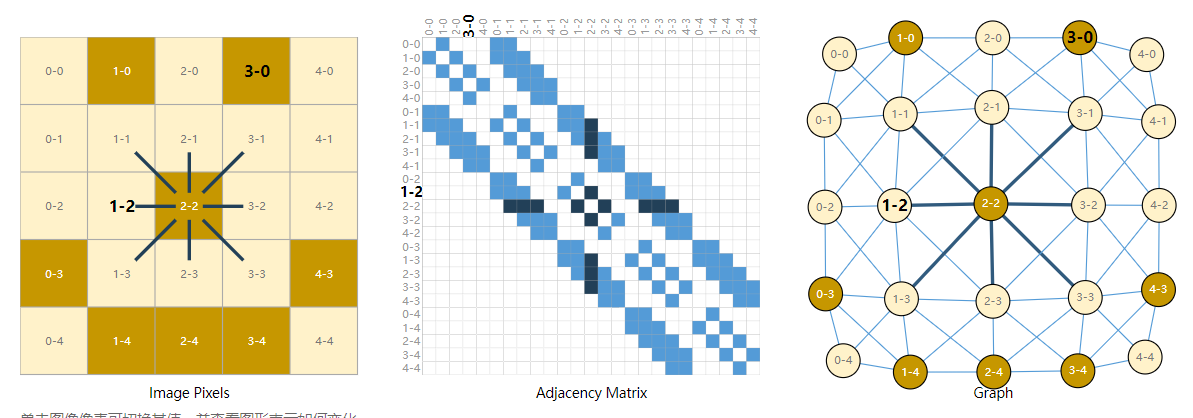
同样的，自然语言处理的语料处理也可以进行图处理，将序列信息转化成有向图结构存储：

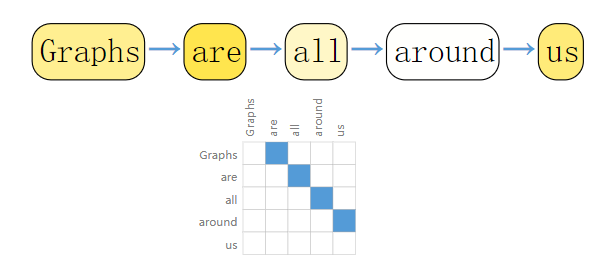
以上的应用例子还有很多，如分子结构、社交网络以及引用文献网络等等。根据图的结构特点，引申出了以下三个目标：

• 求解整体图的信息：常用于进行图像的分类，具有相似图结构的数据归纳为一类；
• 求解节点的向量信息：对某个节点进行预测，类似于图像分割任务，即将同一个图像内的不同物体边界划分出来，预测那一部分属于被切割方。
• 求解边的向量信息：根据已有的点向量表示和全局向量表示，如何求解边，类似于图像生成任务，即将各个物体的相对位置进行确定，之后预测各个对象之间的关系，从而生成符合人类感官的图像。

图神经网络

邻接矩阵作为神经网络中的传递信息的数据结构，存在以下的两个缺点：

• 图往往是稀疏的，这就导致邻接矩阵存储全局信息时，产生大量的空间占用；
• 邻接矩阵存在很多的同分异构体，也就是说特征的组合结果可能会影响邻接矩阵的结构。当同一个图的不同邻接矩阵作为输入获得的模型预测结果可能不一样。

针对问题，采用邻接表存储可以缓解一部分情况，用邻接表代表全局关系，分别用向量表示点集和边集，结合简单的多层感知机，我们获得了最简单的GNN模型：

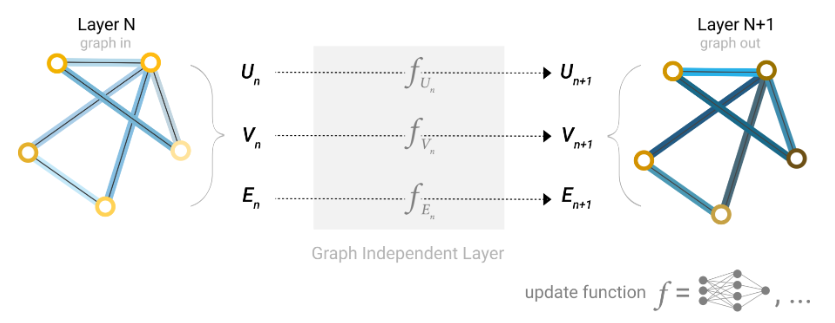
可以看到每一层都有三个多层感知机分别处理UVE，三者互相独立。这种方法明显存在一种问题，假设我需要实现对某一点的预测，而相关的点集不存在该点的信息，我就需要根据相邻E的信息进行预测了。这就是引入的新概念——池化。当然，对边和全局信息的预测也可以进行池化操作。

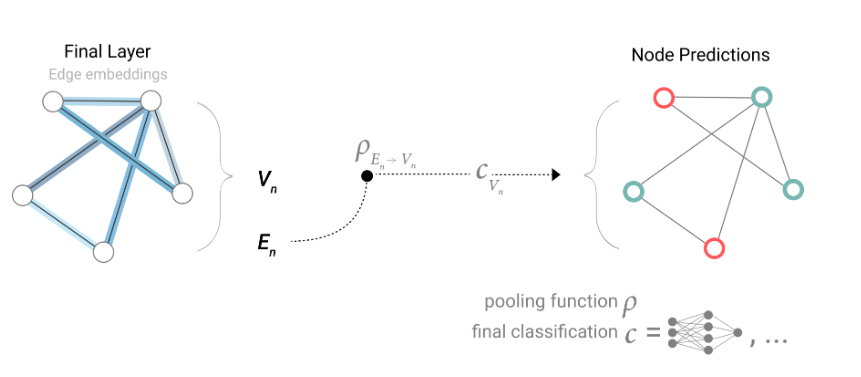
想要在原有网络上实现池化操作，需要保证各集合的相邻信息能够传递，其基本步骤：

• 对图中每个节点，收集相邻节点的嵌入；
• 聚合函数进行消息聚合；（相加、平均或者取最大值）
• 汇集的消息通过更新函数传递；

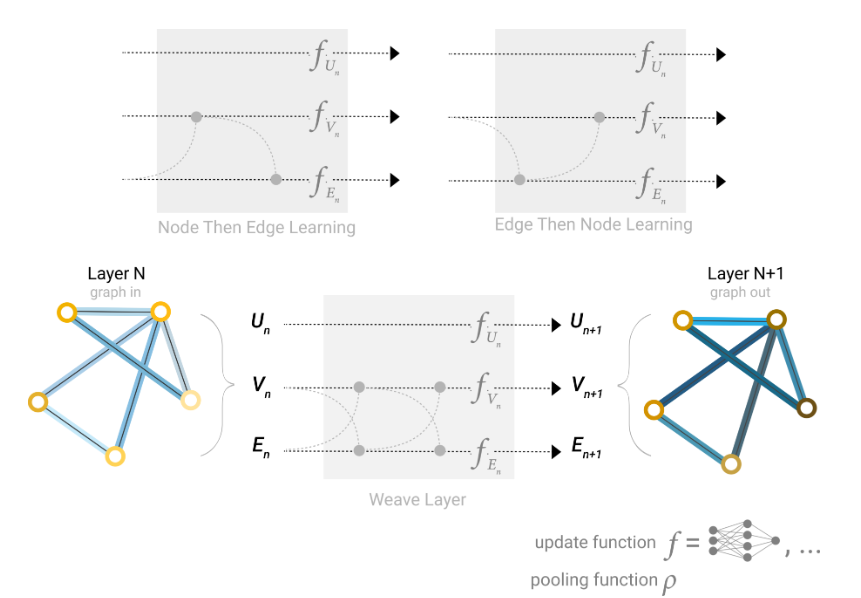
这个过程是三个集合在每层都可以进行的，因此更新的顺序是网络设计的重要一环。

实验

实验部分对GNN在不同影响下的精确度变化：

1.超参数的数量：更多的参数确实和更高的性能相关，但是过高的参数也会影响其性能。

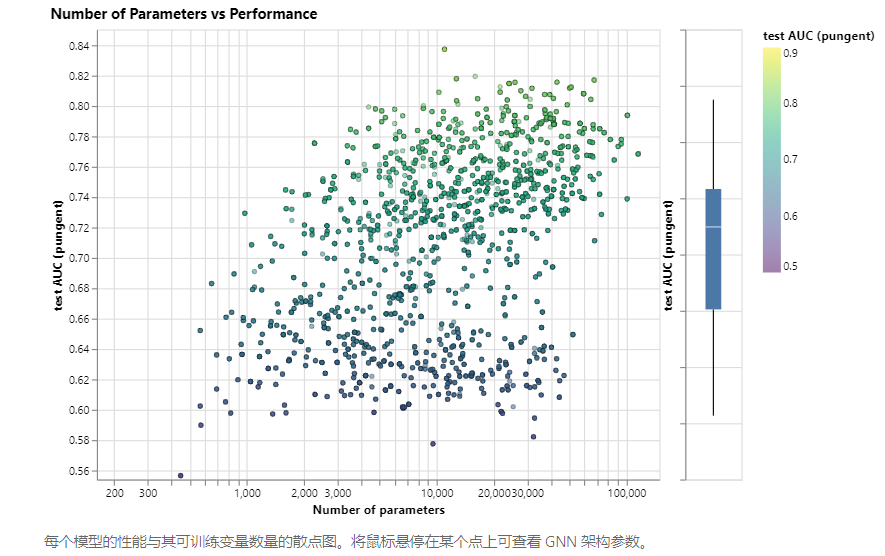
这一部分也可以通过观察不同图属性对性能的影响分布了解到：

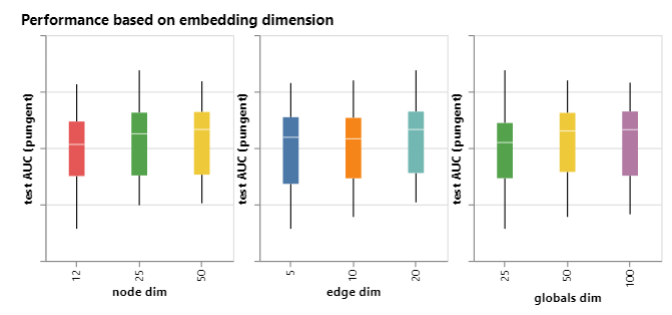
可以看到维度的提升对预测的效果有一定的提升，但是影响不是很大。之后文章对聚合方法、消息传递方法等影响因素进行了研究，其中聚合方法之间相差不大，明显消息传递的方法对模型的影响最大。

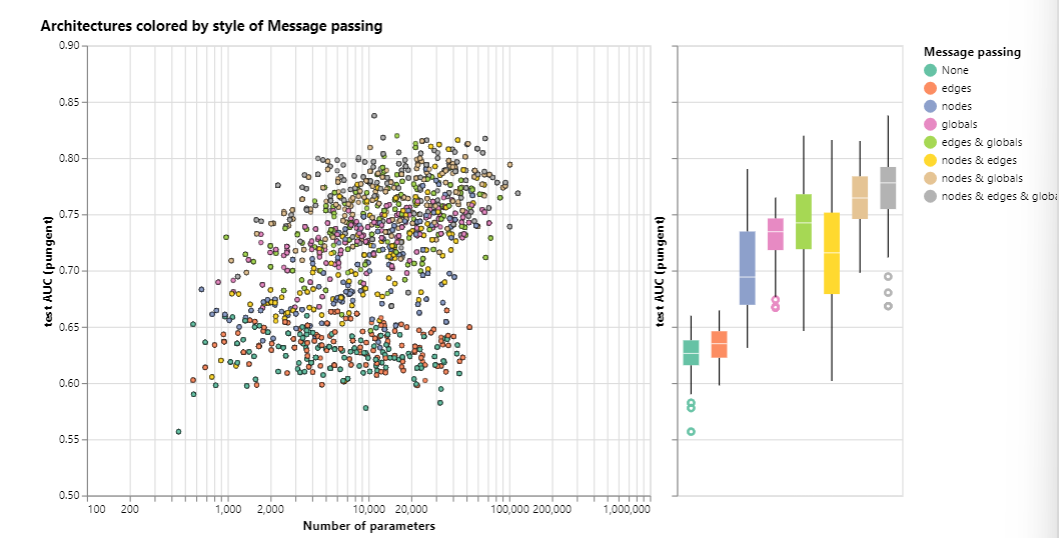
因此，如何进行聚合等方法其实是次要的，最重要的是如何构建图，如何为图注入额外的可以利用的结构和信息，增加能够传递的属性，从而提升模型的性能。这也是未来的发展方向之一。

图相关的技术

在实际的应用领域，还存在这多重图、多边图、超图等等。如何训练和设计具有多种图属性的GNN也是当前的研究前沿领域。

**对比聚合操作：**改进当前的聚合方法（max，mean，sum）；

GCN作为子图近似：对于超图，每一个K层的GCN，在每一层都会往前看一个邻居，最后一个节点看到的是一个子图，这个子图的大小是k，和节点的距离是k。这种方法可以用于解决部分节点长距离的问题；

**边和图对偶：**点集和边集进行替换，保证关系不变的同时进行计算；

**随机游走算法的引入：**图卷积等价于邻接矩阵的矩阵乘法；

**图注意力网络：**邻居节点信息汇聚时进行加权处理（通过注意力机制进行计算）；

生成模型：根据模型的拓扑结构进行有效建模，生成新的数据（graphVAE）；或者使用顺序构建图，从图开始并迭代应用离散操作（graphRNN）；

GNN总结

图神经网络的优化很难实现，同时对超参数非常敏感，因此在工业界落地的实践并不是很多。