diffusion基础论文阅读（更新至NVAE）

diffusion基础论文阅读

主要研究diffusion的三篇入门作，即：

• Deep unsupervised learning using nonequilibrium thermodynamics.
• Improved techniques for training score-based generative models.
• Denoising diffusion probabilistic models

此外，对diffusion的内部架构进行系统的复习：

• VAE模型：Nvae: A deep hierarchical variational autoencoder.
• CLIP文本编码器：Learning transferable visual models from natural language supervision.
• UNET：Long, J., Shelhamer, E., and Darrell, T. (2015). Fully convolutional networks for semantic segmentation.

前置知识

去噪自编码器（Denoising Autoencoder）

实现过程：将有噪声的图片输入Encoder模型，编码成一个低维度的特征，然后通过Decoder模型还原成图片，达到去噪的功能；

基本原理：Score Matching。针对特定的参数进行估计，最小化模型的对数密度梯度和观测数据的对数密度梯度的期望平方距离来估计参数。根据上述的方法，可以分别计算原始数据的概率密度函数和模型的输出概率密度函数，然后比较两个模型的梯度差异，从而实现参数的训练。

带有噪声的数据可以表示为真实数据和噪声的联合分布，对应的目标函数：

$$\begin{aligned} r(y)& =\underset{r}{\operatorname*{\arg\min}}\mathbb{E}_{y\sim p(y),\varepsilon\sim\mathcal{N}(0,\sigma^2I_d)}\left[\|r(y+\varepsilon)-y\|^2\right] \\ &=y+\sigma^2\nabla_y\log\hat{p}(y) \end{aligned}$$

通过移项可以发现r（y）-y实际上就是对带真实噪声的真实分布梯度的估计，然后与Score Matching结合，获得了最终的目标函数：

$$\mathbb{E}_{y\sim p(y)}\mathbb{E}_{\tilde{y}\sim q(\tilde{y}|y)}\left[\left\|s_\theta(\tilde{y})-\nabla_{\tilde{y}}\log q(\tilde{y}\mid y)\right\|_2^2\right]$$

需要注意的是，s函数代表真实带数据的对数密度函数，而后半部分是代表不带噪声的数据在不断添加高斯噪声的这一过程中的对数密度函数。这就是我们常说的diffusion过程。

Langevin Dynamics

朗之万动力学是后续的去噪过程的重要原理。如果想要将一个分布转换为另一个分布，那么可以构建这样一个模型，保证数据每次被处理后各项特征悄然变化，反复进行多次实验，最终得到想要的分布特征。由于每一步的操作都和上一步相关，马尔科夫链的使用也是重要的一环。在Deep unsupervised learning using nonequilibrium thermodynamics一文中给出了具体的推导方法。

Deep unsupervised learning using nonequilibrium thermodynamics

作为开山之作，我这里只对其基本的思想进行了学习整理。

Abstract

机器学习的一个核心问题就是找出数据集的特征概率分布，这个分布往往十分灵活，需要处理的相关项有很多。受非平衡统计物理学的启发，基本思想是通过迭代的正向扩散缓慢破坏数据分布中的结构，然后学习一个反向扩散的过程，回复数据中的结构，从而形成一个高度灵活的生成模型。

Introduction

概率模型一直存在着处理性和灵活性的矛盾：常规的分布具有较高的处理性，能够进行更多的拟合，但是无法恰当描述大规模数据集；灵活的分布能够处理丰富的数据集结构，但是会导致计算成本增加，极端点来说，每拟合一个点就增加一个拟合函数。

这方面的研究在当时发展进度缓慢，作者给出了一种特殊的模型——扩散概率模型。

• 利用马尔科夫链将一个分布逐渐转换成为另一个分布；
• 在每次进行转换时，用小的扰动代替加入函数去改变分布情况；
• 保证得到的数据分布与之前不同；

Algorithm

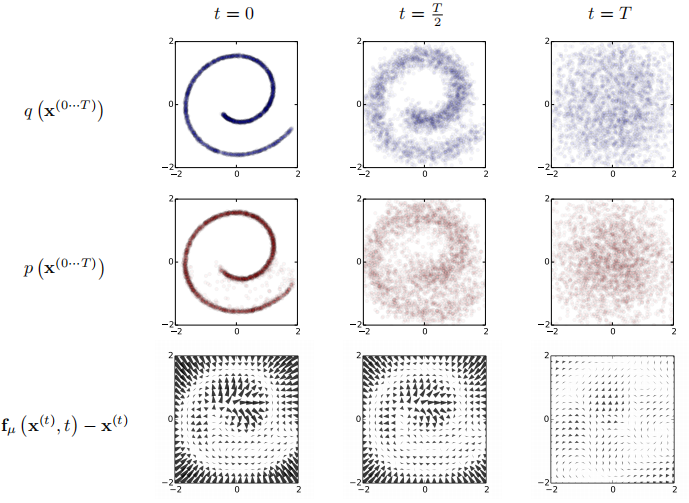
上图是对扩散过程的一个介绍，即如何将源分布向恒等协方差高斯分布转换、恒等协方差高斯分布转换回左端的数据分布、以及扩散过程中的漂移项的变化。

首先是前向传导部分，通过重复应用马尔科夫过程计算某一时刻的分布。进行t步扩散之后的分布表达：

$$q\left(\mathbf{x}^{(0\cdots T)}\right)=q\left(\mathbf{x}^{(0)}\right)\prod_{t=1}^{T}q\left(\mathbf{x}^{(t)}|\mathbf{x}^{(t-1)}\right)$$

对于反向传播，其计算过程恰恰相反：

$$\begin{aligned} p\left(\mathbf{x}^{(T)}\right)& =\pi\left(\mathbf{x}^{(T)}\right) \\ p\left(\mathbf{x}^{(0\cdots T)}\right)& =p\left(\mathbf{x}^{(T)}\right)\prod_{t=1}^{T}p\left(\mathbf{x}^{(t-1)}|\mathbf{x}^{(t)}\right). \end{aligned}$$

随着扩散速率的逐渐衰减，正向扩散和反向扩散具有相同的函数形式。因此在扩散过程相关参数的计算过程中，只需要估计高斯扩散核函数的均值和协方差即可。那么如何将逆过程的求解初始状态用数学进行表示呢？

$$p\left(\mathbf{x}^{(0)}\right)=\int d\mathbf{x}^{(1\cdots T)}p\left(\mathbf{x}^{(0\cdots T)}\right).$$

显然，这个过程计算上是不显示的，因为逆过程的状态变换是无法表示出来的，需要进一步推导得到可以积分的式子：

$$\begin{aligned} p\left(\mathbf{x}^{(0)}\right)& =\int d\mathbf{x}^{(1\cdots T)}p\left(\mathbf{x}^{(0\cdots T)}\right)\frac{q\left(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}\right)}{q\left(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}\right)} \\ &=\int d\mathbf{x}^{(1\cdots T)}q\left(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}\right)\frac{p\left(\mathbf{x}^{(0\cdots T)}\right)}{q\left(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}\right)} \\ &=\int d\mathbf{x}^{(1\cdots T)}q\left(\mathbf{x}^{(1\cdots T)}|\mathbf{x}^{(0)}\right)\cdot \\ &p\left(\mathbf{x}^{(T)}\right)\prod_{t=1}^{T}\frac{p\left(\mathbf{x}^{(t-1)}|\mathbf{x}^{(t)}\right)}{q\left(\mathbf{x}^{(t)}|\mathbf{x}^{(t-1)}\right)}. \end{aligned}$$

之后的数学推导以及数据集实验结果不再赘述。

Conclusion

上文提到的新兴概率分布建模算法在多个真实数据集上证明了有效性。当前的密度估计技术必须牺牲建模能力，这就导致保持可控性和效率的成本较大。本文算法的核心是估计一个马尔科夫扩散链的反转，每个扩散阶段的反转分布十分容易估计。

Improved techniques for training score-based generative models.

参考博客：Improved Techniques for Training Score-Based Generative Models论文阅读-CSDN博客

Abstract

现有的生成模型在低维空间能够给出高质量的图像样本，但是在高维空间是不稳定的，因此给出了一种新的理论方法，在阐述失败方法的错误原因的同时，给出跨越数据集的推广方案。

Conclusion

通过改善训练和采样过程，获取更好地样本质量，从而以高分辨率生成高保真的图像。

Denoising Diffusion Probabilistic Models

Abstract

根据链接扩散概率模型以及涉及去噪分数匹配的朗之万动力学，训练加权的变分界设计，渐进地处理数据。

Introduction

score matching的发展对VAE的图像生成产生了深渊影响，从而达到GAN的水平。

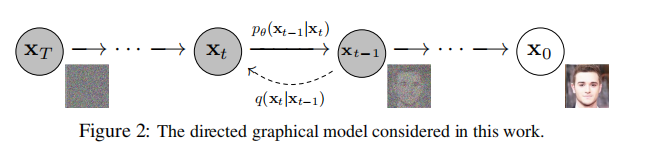
这里作者认为突出工作是将训练过程中在多个噪声水平上的去噪分数匹配和朗之万动力学应用的等价性，正是因为这种等价性，方便了参数估计的计算，从而得到分布概率。最后作者强调了一下扩散模型的渐进解码过程，概括自回归模型通常可能得情况。

Background

对于分布p而言，他被定义为一个马尔科夫链，逆向去噪计算：

$$p_\theta(\mathbf{x}_{0:T}):=p(\mathbf{x}_T)\prod\limits_{t=1}^Tp_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)\\ \quad p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t):=\mathcal{N}(\mathbf{x}_{t-1};\boldsymbol{\mu}_\theta(\mathbf{x}_t,t),\boldsymbol{\Sigma}_\theta(\mathbf{x}_t,t))$$

对于分布q而言，他作为后验概率也是一个马尔科夫链，正向添加高斯噪声：

$$q(\mathbf{x}_{1:T}|\mathbf{x}_{0}):=\prod_{t=1}^{T}q(\mathbf{x}_{t}|\mathbf{x}_{t-1}),\quad q(\mathbf{x}_{t}|\mathbf{x}_{t-1}):=\mathcal{N}(\mathbf{x}_{t};\sqrt{1-\beta_{t}}\mathbf{x}_{t-1},\beta_{t}\mathbf{I})$$

很明显，我们需要对x0状态下的分布进行计算，这个过程是通过优化负对数似然的通常变分界实现的。

$$\mathbb{E}\left[-\log p_\theta(\mathbf{x}_0)\right]\leq\mathbb{E}_q\bigg[-\log\frac{p_\theta(\mathbf{x}_{0;T})}{q(\mathbf{x}_{1;T}|\mathbf{x}_0)}\bigg]=\mathbb{E}_q\bigg[-\log p(\mathbf{x}_T)-\sum_{t\geq1}\log\frac{p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)}{q(\mathbf{x}_t|\mathbf{x}_{t-1})}\bigg]=:L$$

可以发现，当衰减参数值β很小时，两个函数的有相同的形式。

Conclusion

我们使用扩散模型提供了高质量的图像样本，并发现了扩散模型和变分推理之间的训练马尔可夫链、去噪分数匹配和退火朗之万动力学（以及基于能量的扩展模型）、自回归模型和渐进有损压缩之间的联系。

阶段总结

去噪扩散概率模型（Denoising Diffusion Probabilistic Model，DDPM阅读笔记）—理论分析1 - 知乎 (zhihu.com)

VAE模型

核心思想：通过构造编码器和解码器，使得图片能够编码成易于表示的形态，并且这一形态能够尽可能无损地解码回原真实的图像。举个例子，对于一张满月照片和一张半月照片，对其进行编码解码过程，得到了两种图片的隐式表示。此时，我想要对半月图片进行生成，那么就是在两个隐式表示的向量之间选择一个点进行生成。

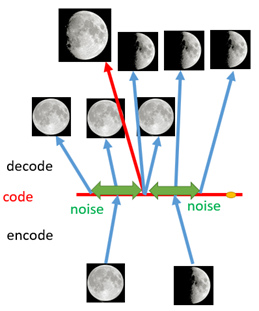
在生成过程中，往往会出现某些点不在训练时的特征空间中，这时就需要对训练数据增加噪声从而使得隐式表示的范围更大，未包含的点可以通过计算和隐式表示之间的距离相似度进行生成。但是基础的VAE得到的图像效果并不是很好。

NVAE: A Deep Hierarchical Variational Autoencoder

code：https://github.com/NVlabs/NVAE.

Abstract

背景：深度学习生成常见的四种模型：归一化流、自回归模型、变分自编码器以及基于深度能量的模型。目前VAE框架关注于如何应对统计上的挑战，作者关注于分层VAE的神经网络架构的正交方向，提出了NVAE的方法使用深度可分离卷积和批量归一化来生成图像。NVAE配备了正态分布的残差参数化，并且训练通过谱正则化来稳定。

Introduction

先前的研究围绕统计学的问题，即近似后验和真实后验分布之间的差距、制定更加严格的边界、减少梯度噪声等等，对架构的改动很少。本文提出的是一种深度分层的VAE模型，缩小了和自回归模型之间的差距。

在原始的模型中添加BN层是使得深度VAE成功的重要因素，但是众多的BN层不能解决训练不稳定的结果。因此，本文提出了两个创新点：

• 提出了一种近似后验参数的残差参数化的方法，用以改善KL项的消失问题。
• 证明光谱正规化是稳定VAE训练的关键。

本文的工作借鉴了IAF-VAE模型，不同点在于近似后验进行了参数化，同时训练扩展到了更大的图像。

Background

传统的VAE模型关注于如何求解p(x,z) = p(z)p(x|z)，其中p(z)代表z的先验分布，p(x|z)是给定潜在变量z生成数据x的似然函数。这里作者对隐层表示进行了正则化处理，将整体空间划分为l个变量，得到新的VAE计算公式：

$$\mathcal{L}_{\mathrm{VAE}}(\boldsymbol{x}):=\mathbb{E}_{q(\boldsymbol{z}|\boldsymbol{x})}\left[\log p(\boldsymbol{x}|\boldsymbol{z})\right]-\mathrm{KL}(q(\boldsymbol{z}_1|\boldsymbol{x})||p(\boldsymbol{z}_1))-\sum_{l=2}^{L}\mathbb{E}_{q(\boldsymbol{z}_{<l}|\boldsymbol{x})}\left[\mathrm{KL}(q(\boldsymbol{z}_l|\boldsymbol{x},\boldsymbol{z}_{<l})||p(\boldsymbol{z}_l|\boldsymbol{z}_{<l}))\right]$$

可以看到，最后一部分将p(z)和q(z|x)进行了拆解，防止后续的散度发生消失问题。为了求解上述的p(z)和q(z|x)，需要构建自上而下的双向模型分别计算x和z的表示。

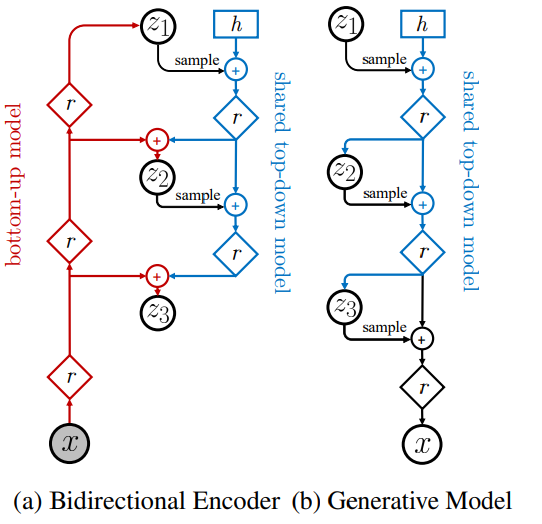
Method

NVAE引入的残差单元更新了网络架构，同时加入了后验参数化和稳定训练解决方案。

残差单元的引入：

背景：为了解决长距离相关性问题，可以深度多层次多尺度构建VAE，每组潜在变量逐层采样，捕捉层级结构之间相似性以及同一层次的局部相似性；也可以增大感受野，增加卷积核的大小。

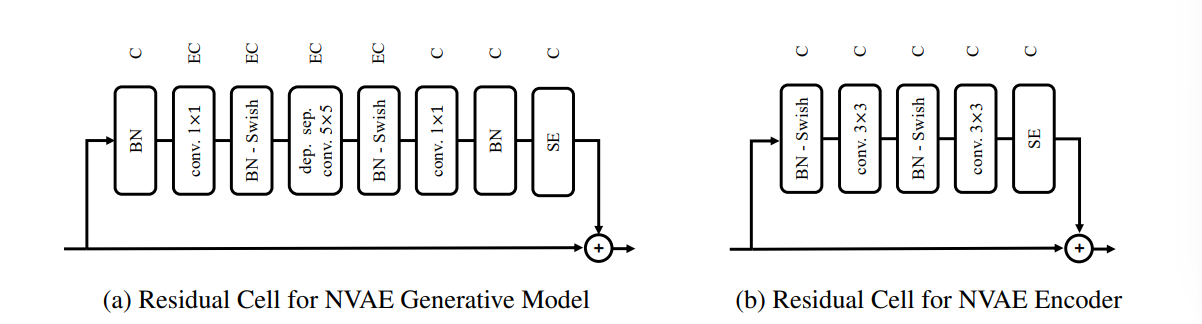
首先分析加入残差单元的NVAE生成模型结构。首先是BN层对数据进行归一化处理，然后使用1×1的卷积核扩充通道数，利用switch激活函数激活，接着对特征进行提取，采用的是5×5的卷积核。处理完成后利用switch函数激活结构，利用1×1卷积转换通道数，完成归一化，最后引入SE模块（https://blog.csdn.net/qq_42617455/article/details/108165206，对结果进行激励，提高参数的数量）。

对于编码器部分，减小内存提高效率，没有对通道数进行更改，只使用了常规的卷积。

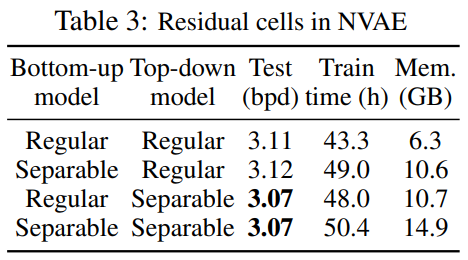
上述结构中，我认为最为创新的就是BN和switch层混合减小运行内存，只为后向传递存储一个特征图。

KL散度消失问题的解决方案：

先验分布如果发生移动，近似后验值也会发生相应移动，因此得到如下：

$$p(z_l^i|\boldsymbol{z}_{<l}):=\mathcal{N}\left(\mu_i(\boldsymbol{z}_{<l}),\sigma_i(\boldsymbol{z}_{<l})\right) \\ q(z_l^i|\boldsymbol{z}_{<l},\boldsymbol{x}):=\mathcal{N}\left(\mu_i(\boldsymbol{z}_{<l})+\Delta\mu_i(\boldsymbol{z}_{<l},\boldsymbol{x}),\sigma_i(\boldsymbol{z}_{<l})\cdot\Delta\sigma_i(\boldsymbol{z}_{<l},\boldsymbol{x})\right)\\ \operatorname{KL}\left(q(z^i|\boldsymbol{x})||p(z^i)\right)=\frac12\left(\frac{\Delta\mu_i^2}{\sigma_i^2}+\Delta\sigma_i^2-\log\Delta\sigma_i^2-1\right),$$

在重新规划好KL散度的计算过程之后，KL散度仍存在无法确定边界的问题。这里可以通过正则化Lipschitz常数来保证编码器预测的潜在表示有界（Lipschitz可以理解为连续函数的导函数最大值，这个值越低，KL散度更有可能有界）。对于Lipschitz常数的计算，可以通过SR方法对权重矩阵进行SVD分解，限制最大的奇异值为1，从而满足1-Lipschitz条件。

Conclusions

除了上述的工作，本文还提出了减少VAE内存使用的方法，提高了训练速度。因为VAE模型在实际训练中更加忠于原始的数据分布，不会产生像GAN一样的模式崩溃问题，因此VAE才是我们的未来！（我最喜欢的拉踩环节）

https://blog.csdn.net/RicardoHuang/article/details/124957814

Future Work

生成式学习的中偏差校正是一个活跃的研究领域，说不定可以balance一下数据集整点不一样的反例。

Learning transferable visual models from natural language supervision.

Abstract

CLIP是一种基于对比文本-图像对的预训练方法。传统的计算机视觉任务是预测一组固定的物体类别，这种监督形式的模型泛用性交叉。本文使用从图像和原始文本中学习的方法，构建了基于图片和标题匹配的模型。经过预训练，自然语言可以引用所学的视觉概念实现模型在下游任务中的zero-shot transform。

Introduction

**近些年来nlp领域的pretrain实现了基于庞大语料库的语义能力理解，因此能够在上游构建一个与任务无关的架构，在下游实现zeroshot的学习。**但是计算机视觉领域仍旧使用特定情况特定分析的方法。之前也进行过对I2T的工作：

• 使用CNN实现预测图像标题中的单词、n元短语；
• transformer的使用mask进行语言建模，从文本中学习图像表示；

本文综合之前的研究，缩小了和SOTA之间的差距，其基本实现是一个简化版本的ConVIRT模型。综上所述，本文提出的CLIP模型具有以下两个创新点：

• 泛用性：在OCR、地理定位和动作识别等特定领域都优于ImageNet；
• 鲁棒性：相较于ImageNet更加稳健；

Approach

数据集构建

现有：MS-COCO ， Visual Genome ，YFCC100M

结论：和现有的nlp预训练相比，合乎标准的数据太少，因此作者自己构建了一个包含4亿对数据的数据集，每组文本查询在2000对数据左右。

预训练方法确定

**最初方案：从头开始训练图像CNN和encoder来预测图像的标题，但是对海量数据的训练效率明显低于相同文本的词袋编码。

**最终方案：**对比训练降低时间成本，从单词匹配到文本和图片匹配。

**基本方法：**给定一批N个图像文本对，CLIP被用来预测批次中N×N个的可能配对中哪一个实际发生。

• 图像encoder和文本encoder将两组数据传入多模态嵌入空间，计算余弦相似度，最大化前N个相似度。
• 针对得到的相似性分数，优化对称交叉熵损失。
• 图像encoder：简化图像转换函数、数据增强方法。本文作者给出了两种架构：
  • ResNet+Antialiased rect-2 blur pooling+Attention：在保持平移不变性的同时，减少深度学习模型中的aliasing效应（高频的信号被混入到低频的信号中）。这种方法的主要思想是在最大池化层和下采样层之间插入一个低通滤波器，以尽可能地保留平移不变性。此外全局平均池化层也被替换成为注意力机制。
  • ViT：在位置编码部分添加了归一化层，更换了新的参数初始化方法。
• 文字encoder：非均匀采样文本中的句子。
  • transformer架构：12层架构，多注意力头。最终输出结果经过层归一化后线性投射到多模态嵌入空间中。

在检验模型性能的方向上，本文考虑到下游的大多数计算机视觉研究都侧重于表层研究，因此使用最常见的linear probe control判断模型的预测结果。

**linear probe control：**在预测阶段，将模型的最后一层替换成线性层，只训练这个线性层就是linear probe。通过最后分类器给出的准确率判断模型的质量。

Analysis

这里就是着重强调了一下CLIP模型在下游任务中的zeroshot获得了和券监督baseline的同等性能。

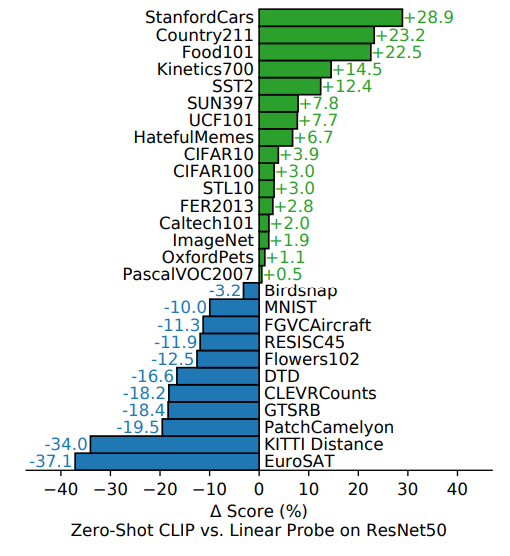
此外，本文不仅在数据集上实现了zeroshot，还对fewshot进行了研究，和其他模型进行对比：

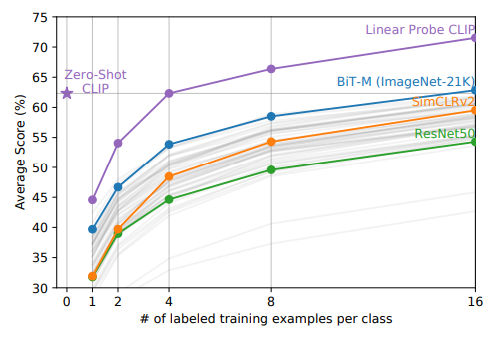
可见，CLIP的zeroshot的性能与相同特征空间上的四次逻辑回归不相上下。

Conclusion

本文研究了如何将自然语言处理中的特定任务移植到计算机视觉领域。在了优化训练目标，CLIP在预训练期间学习各种任务，这种任务学习通过自然语言promt加以利用，实现了许多数据集的zero-shot。虽然能够和特定任务监督模型相媲美，但依旧存在很大的改进空间。

总结

这一部分对diffusion模型的网络架构进行了了解，之后会单开一篇阅读一下ViT的论文，这一部分就看李沐老师的视频学习一下了。此外，SD的学习以及之后的四个研究方向会新开一篇进行研究，同时对于SD和CLIP的分析看一下能不能加上对源码的理解。