每日一题整理——2023.11
前言
这个月整理的题目比较少,一方面是偷懒了,另一方面就是以后只做中文站的题了,一天两道太浪费时间了。
题
11.4
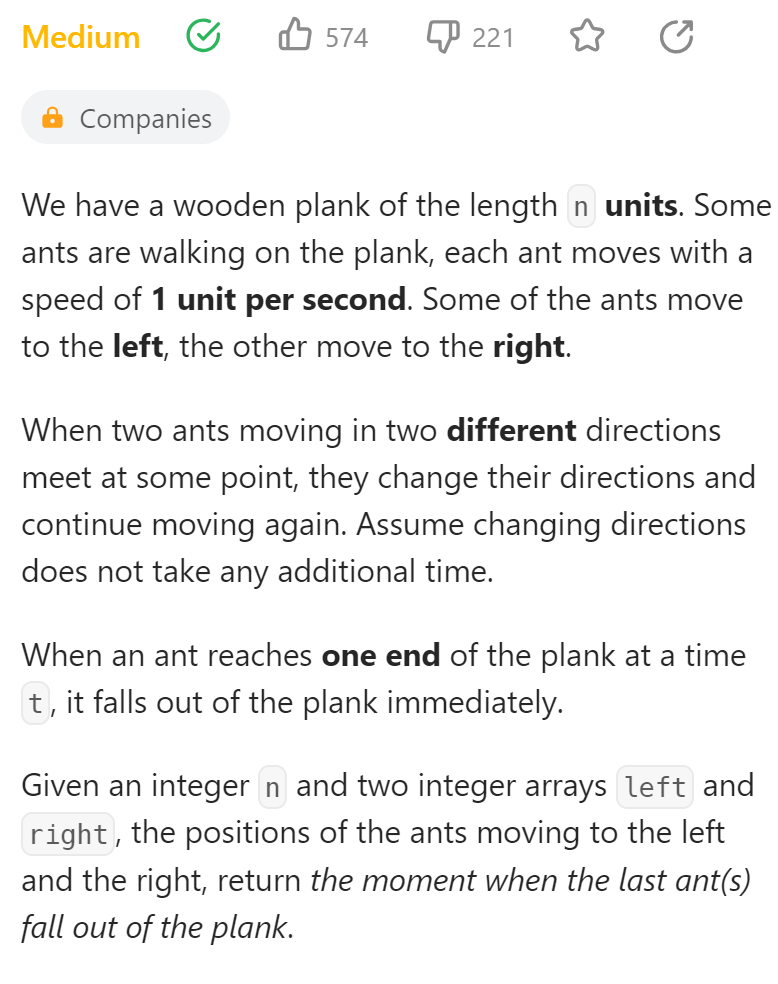
数据范围:

我的思路:
这道题很有意思,初看我以为是模拟,但是后来想了想,对于每一对发生碰撞的蚂蚁而言,碰撞之后发生反向并不会影响最后两边到达的蚂蚁数量。简单来说,就是无论是否发生碰撞,对于每一只蚂蚁而言到达的时间只和初始位置有关。(这里我们认为碰撞之后蚂蚁的身份互换)
class Solution {
public:
int getLastMoment(int n, vector<int>& left, vector<int>& right) {
int ans = 0;
int nn = left.size();
int m = right.size();
for(int i = 0 ; i < nn ; ++i){
ans = max(ans , (abs(0-left[i])));
}
for(int i = 0 ; i < m ; ++i){
ans = max(ans , (abs(n-right[i])));
}
return ans;
}
};
11.6

数据范围:

我的思路:
位运算获取字符串表达,然后按位与进行计算,从而判断两个字符串是否存在重复字符。这里重要的是字符串转换成二进制数表示的方法。
class Solution {
public:
int maxProduct(vector<string>& words) {
int n = words.size();
unordered_map<int , int> mp;
for(int i = 0 ; i < n ; ++i){
int mask = 0;
string word = words[i];
int length = word.length();
for(int j = 0 ; j < length ; ++j){
mask |= 1<<(word[j]-'a');
}
if(mp.find(mask) != mp.end()){
if(length > mp[mask]){
mp[mask] = length;
}
}
else{
mp[mask] = length;
}
}
int ans = 0;
for(auto it : mp){
int len = it.second;
for(auto item : mp){
if(((it.first) & (item.first)) == 0){
int len1 = item.second;
ans = max(ans , len*len1);
}
}
}
return ans;
}
};
11.8
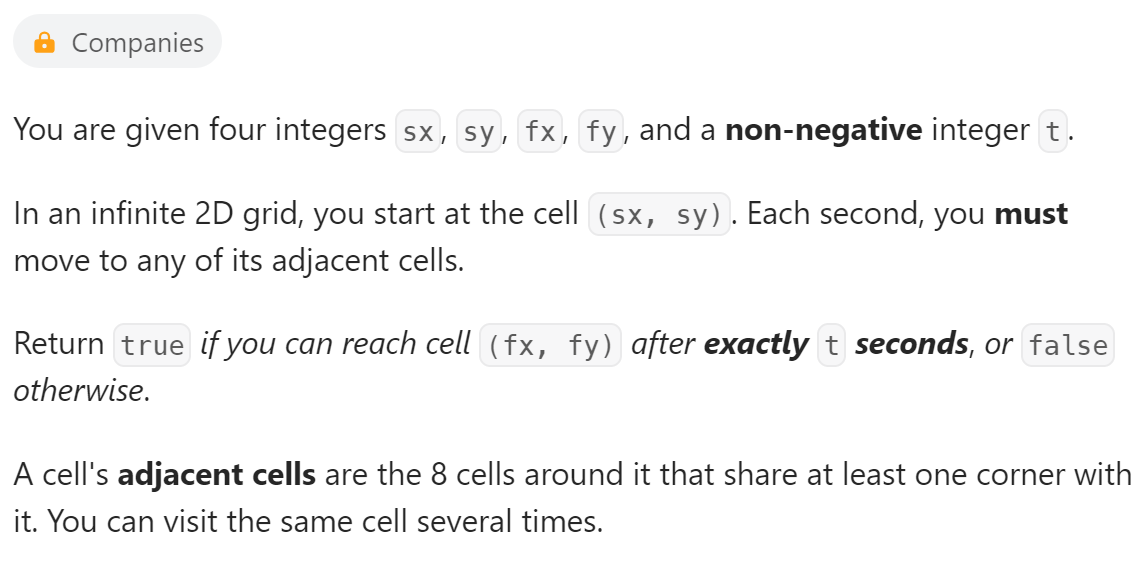
数据范围:

我的思路:
基本思想就是找出最小的步数,所有的解决方案都是大于等于最小步数的。当然,对于特殊的边界需要着重考虑。这道题之所以浪费了一些时间主要是边界找错了,首先将起点和终点限制为某一个二维数组找左上角到右下角的最短距离,这一步求解最小步数并没有问题,但因为纠结于二维数组的限制,忘了其实坐标系内并没有边界,因此犯下了计算最大步数的错误。
class Solution {
public:
bool isReachableAtTime(int sx, int sy, int fx, int fy, int t) {
int m = abs(sx-fx)+1;
int n = abs(sy-fy)+1;
int min_step = n + max(0 ,m-n) - 1;
if(min_step == 0){
return t == 1 ? false : true;
}
if(t < min_step){
return false;
}
return true;
}
};
11.9

数据范围:

我的思路:
数据范围很小,但是我第一次提交还是TLE了。这里基本的思路是计算每个空地的着火事件,利用fire二维数组存储,然后使用二分搜索确定最终的等待时间。假设等待时间为t,那么t时刻从起点出发,广度优先搜索可能得路径,最终得到结果。
struct Node{
int x;
int y;
int t;
Node(int xx , int yy , int tt){
x = xx;y = yy;t = tt;
}
};
class Solution {
public:
constexpr static int fx[4] = {0,0,1,-1};
constexpr static int fy[4] = {1,-1,0,0};
void bfs(vector<vector<int>>& fire , vector<vector<int>>& grid , int x , int y){
int m = grid.size();
int n = grid[0].size();
queue<Node> q;
q.push(Node(x,y,0));
while(!q.empty()){
int nn = q.size();
while(nn--){
Node tmp = q.front();
q.pop();
for(int i = 0 ; i < 4 ; ++i){
int xx = tmp.x + fx[i];
int yy = tmp.y + fy[i];
if(xx>=0 && yy>=0 && xx<m && yy<n && grid[xx][yy] == 0 && (fire[xx][yy] == INT_MAX || fire[xx][yy] > tmp.t+1)){
fire[xx][yy] = min(fire[xx][yy] , tmp.t+1);
q.push(Node(xx,yy,fire[xx][yy]));
}
}
}
}
}
bool check(vector<vector<int>>& fire , vector<vector<int>>& grid , int time){
int m = grid.size();
int n = grid[0].size();
int t = time;
vector<vector<int>> v(m,vector<int>(n));
queue<Node> q;
q.push(Node(0,0,t));
v[0][0] = true;
while(!q.empty()){
int nn = q.size();
while(nn--){
Node tmp = q.front();
q.pop();
for(int i = 0 ; i < 4 ; ++i){
int xx = tmp.x + fx[i];
int yy = tmp.y + fy[i];
if(xx>=0 && yy>=0 && xx<m && yy<n){
if(v[xx][yy] || grid[xx][yy] == 2){
continue;
}
if(xx == m-1 && yy == n-1){
return fire[xx][yy] >= tmp.t+1;
}
if(fire[xx][yy] > tmp.t+1){
q.push(Node(xx,yy,tmp.t+1));
v[xx][yy] = true;
}
}
}
}
}
return false;
}
int maximumMinutes(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> fire(m,vector<int>(n , INT_MAX));
for(int i = 0 ; i < m ; ++i){
for(int j = 0 ; j < n ; ++j){
if(grid[i][j] == 1){
fire[i][j] = 0;
bfs(fire,grid,i,j);
}
}
}
int ans = -1;
int left = 0 , right = m*n;
while(left <= right){
int mid = left + (right-left)/2;
if(check(fire,grid,mid)){
ans = mid;
left = mid+1;
}
else{
right = mid-1;
}
}
return ans >= m*n ? 1e9 : ans;
}
};
11.18

数据范围:

我的思路:
这道题重点在于如何解决在遍历过程中起点的重新确定,这里想的时间有点长了,因此记录一下。
class Solution {
public:
int maxFrequency(vector<int>& nums, int k) {
int n = nums.size();
sort(nums.begin() , nums.end());
long long i=0 , j=0 , sum=0 , ans=0;
for(i = 0 ; i < n ; ++i){
sum += nums[i];
while((i-j+1)*nums[i] - sum > k){
sum -= nums[j];
++j;
}
ans = max(ans , i-j+1);
}
return (int)ans;
}
};
11.19

数据范围:

我的思路:
基本思想是构建滑动窗口去计算每个区间的最大值,但是之前没有做过变化边界的窗口滑动,因此记录一下。这里的重点在于对tmp_sum的保存上,构建了三个max_sum,分别表示第一个、前两个、所有的最大值,按照顺序分别更新即可。
class Solution {
public:
vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k) {
vector<int> ans;
int sum1 = 0 , max_sum1 = 0 , max_index1 = 0;
int sum2 = 0 , max_sum12 = 0 , max_index12_1 = 0 , max_index12_2 = 0;
int sum3 = 0 , max_Total = 0;
for(int i = k*2 ; i < nums.size() ; ++i){
sum1 += nums[i-k*2];
sum2 += nums[i-k];
sum3 += nums[i];
if(i >= k*3-1){
if(sum1 > max_sum1){
max_sum1 = sum1;
max_index1 = i-k*3+1;
}
if(max_sum1 + sum2 > max_sum12){
max_sum12 = max_sum1 + sum2;
max_index12_1 = max_index1;
max_index12_2 = i-k*2+1;
}
if(max_sum12 + sum3 > max_Total){
max_Total = max_sum12 + sum3;
ans = {max_index12_1 , max_index12_2 , i-k+1};
}
sum1 -= nums[i-k*3+1];
sum2 -= nums[i-k*2+1];
sum3 -= nums[i-k+1];
}
}
return ans;
}
};