发布日期: 2021-04-12

作者: xhsioi

文章字数: 5k

阅读时长: 17 分

阅读次数:

结合美赛题目的图论学习

导入

什么是图论？

图论(Graph Theory)是离散数学的一个分支。它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

关于图论的最早文字记录出现在1736年瑞士数学家欧拉的论著中，也就是著名的戈尼斯堡七桥问题。戈尼斯堡是东普鲁士的首都（位于今天的俄罗斯加里宁格勒市），普赖格尔河流过该城市，这条河上建有七座桥将河中间的两座小岛（A、B）和两岸(C、D) 连接。有人提出来：能否每座桥都只走一遍，最后回到出发点。很多人曾尝试过，但最终都没有成功。1736年有人带着这个问题找到了大数学家欧拉，欧拉把两座小岛和河的两岸分别看作四个点，把七座桥看作这四个点的连线，经过进一步分析，得出结论：不可能每座桥都走一遍，最后回到原点，并给出了所有线路应具备的条件。这项工作使得欧拉成为了图论的创始人。

生活中具体的例子？

最短路径问题：

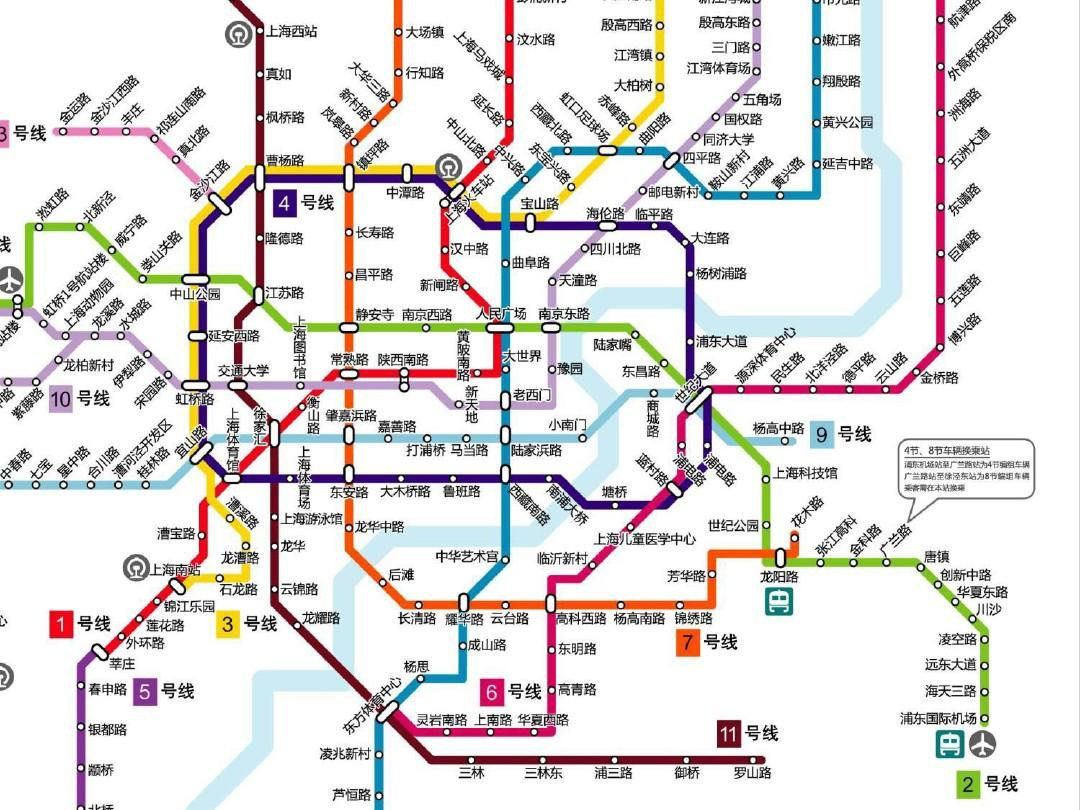
对于十分复杂的网络，就像地铁线路，每个站点就是图的顶点，站点之间有通车就画一条边。每一条边的权重为对应两个端点之间的距离、时间、票价。

我们在两个地点之间进行通勤时，通常我们会选择总票价最少的路线，或者时间最少的路线，或者距离最短的路线，而这里就是图论的应用–最少最短即为最短路径。

着色问题：

对地图进行着色，如何使相同颜色的区域分离？
多叉路口如何设计信号灯管理系统？
…

最小生成树：

某一地区有若干个主要城市,现准备修建高速公路把这些城市连接起来.假定已经知道了任意两个城市之间修建高速公路的成本,那么应如何决定在哪些城市间修建高速公路,使得总成本最小?

旅行商问题、拉姆齐问题等等…

以上图论的经典问题同学们可以在例会之后进行更深入的了解。

图论的基本概念

图的概念：

定义一个图G是指一个二元组(V(G),E(G))，其中:

$V(G)=\left\{v_{1}, v_{2}, \ldots, v_{\nu}\right\}$ 是图中顶点构成的集合，每个顶点有着对应的编号。
$E(G)$ 称为由顶点集中的任意相邻两点构成的边的集合，称为边集。

图的分类：

有向图（Digraph）：图中的每条边都带有方向，称为有向图。
无向图（Undirected graph）：图中的每条边都没有方向，称为无向图。
赋权图（Weighted graph）：图中的每条边都有一个或多个对应的参数，称为赋权图。该参数称为这条边的权，权可以用来表示两点间的距离、时间、费用。

图的矩阵表示：

邻接矩阵：

对于无向图G，其邻接矩阵 $A=\left(a_{i j}\right)_{V \times V}$ ，其中：

对于有向图 $G=(V,E)$ ，其邻接矩阵 $A=\left(a_{i j}\right)_{V \times V}$ ，其中：

对于有向图赋权图 $G=(V,E)$ ，其邻接矩阵 $A=\left(a_{i j}\right)_{V \times V}$ ，其中：

对于无向赋权图的临街矩阵可以类似定义。

最短路问题

Dijkstra算法

什么是Djikstra?

一句话概括就是：
Dijkstra:给定一个顶点，可以求得其到其他所有顶点的最短路径长度。

基本思想：

D的初始状态为：如果从源点s到顶点v有弧则D[v]记为弧的权值；否则将D[v]置为无穷大。(构建邻接矩阵)
每次从尚未确定最短路径长度的集合V-S中取出一个最短特殊路径长度最小的顶点u，将u加入集合S，同时修改数组D中由s可达的最短路径长度：若加进u做中间顶点，使得vi的最短特殊路径长度变短，则修改vi的距离值（即当D[u] + W[u, vi] < D[vi]时，令D[vi] = D[u] + W[u, vi]）。
然后重复上述操作，一旦S包含了所有V中的顶点，D中各顶点的距离值就记录了从源点s到该顶点的最短路径长度。

结合具体例题来看一看吧：

这里初始的起点为 $v_0$ ，我们根据步骤一步步来：

1.构建邻接矩阵：

2.构建图表求解v0到各点的最短路径：

当然，Dijkstra算法并不是万能的，如下图所示，假如图中存在负边，部分情况Dijkstra可求解，但有时候也会出现问题：

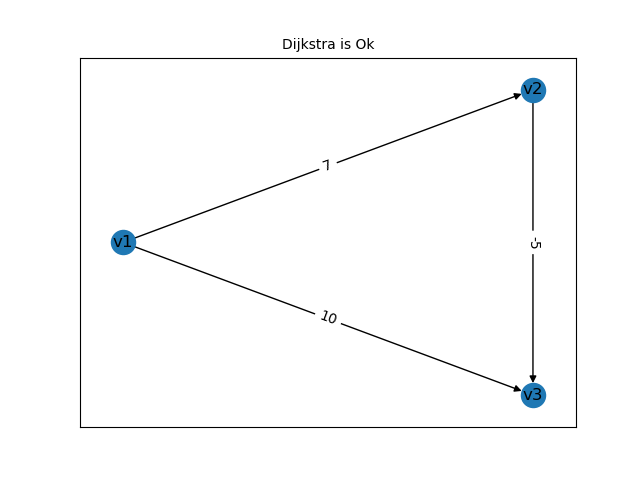
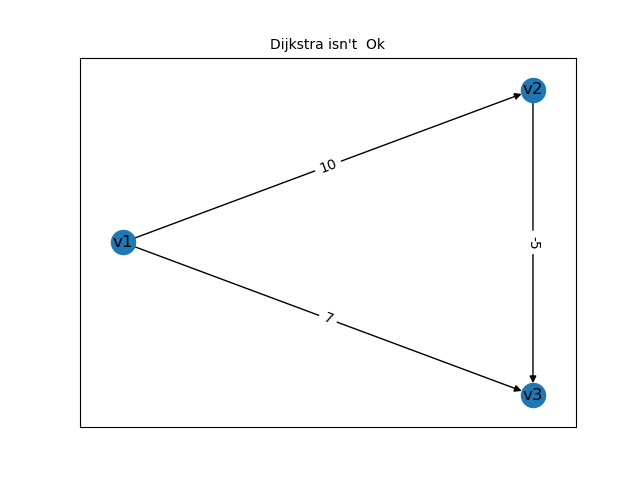
上图中，如果以v1为起点，第二张图的Dijkstra算法就会出现问题：

v1到v3的最短距离为7.

具体计算根据上方运算即可。

这时候，我们可以选择Bellman-Ford，SPFA， Floyd等算法进行求解，当然它们也存在着部分缺点，如下：

算法	优点	缺点
Dijkstra	适合用于稠密图	不能处理负权边
Bellman-Ford	可以处理负环	时间复杂度较高，不适合处理大规模数据
Floyd	适合用于稀疏图	可以处理负权边，但是不能处理负环
SPFA	能够解决负环、负权边的问题	时间复杂度较高。

对于最短路算法的介绍就到这里。最短路算法只是图论的冰山一角，甚至算不上一角，可以说得上是最小的子模型了，因此你需要了解它的基本实现原理，做到在比赛中根据题设迅速改出你想要的模型。

可以看出，图论更加关注于点与点之间的关系问题。千言万语，无论题设怎样变化，最后归根到底就是点与点的相连的那几条边。

结合近三年的美赛D题，我们不难发现某些端倪：

在2020年的美赛D题中，解题的关键在于足球队中各个队员如何传球、最后的传球情况；
在2021年的美赛D题中，解题的关键在于形成相似度指标之后，如何利用相似度指标构建有向音乐网络，进行社会网络分析。
在2022年的美赛D题中，解题的关键在于员工、技术、流程三大指标的相互影响的结果。

可以看出，从稍加分析就能看出利用网络流建立传球网络，到先对数据进行分析、特征提取再形成音乐网络，再到今年先评价后网络分析，虽然题目越来越综合，但是其本质还是没有变，主题总是能够抽象为图/网络中相邻结点之间的关系。

总而言之，得图论者，得美赛D题。（暴论）

图论部分就介绍到这里，其它如旅行商问题、最小生成树的代码我会放到附件中，供大家学习。

网络相关知识

什么是网络？

由更多节点、更多连线构成的更为复杂的图；

注意：这里的本质还是图，这一部分我们只是更为深入地了解这种特殊图的性质，因此之前的算法都是适用的。

对于节点：

度：

在无向图中，度代表与这个节点连接的边数；
在有向图中：
- 所有指出该节点的边的数量，称为该节点的出度；
- 所有指向该节点的边的数量，称为该节点的入度；
- 入度和出度的和称为度

关于度的问题，我们可以在社交网络中进行举例。

对于无向图，我们规定社交网络中各点之间的关系为”是否认识“，显而易见，当你认识的人越多、你对应的度就会越大，你越有可能称为整个网络的中心。

对于有向图，我们规定社交网络中各点之间的关系为“A是否喜欢B”，此时，当喜欢你的人数越来越多，或者你喜欢的人越来越多，那么你对应的入度/出度就会越大，你就越有可能称为网络中最受欢迎/最受人讨厌的中心。

节点的性质：

**度中心性：**度中心性（Degree Centrality）是在网络分析中刻画节点中心性（Centrality）的最直接度量指标。一个节点的节点度越大就意味着这个节点的度中心性越高，该节点在网络中就越重要。

对于一个拥有g个节点的无向图，节点i的度中心性是i与其它g-1个节点的直接联系总数，矩阵表示如下：

关于度中心点的应用研究：

在各种社会关系网络(如你的朋友圈子、BBS 和微博等在线社区)中，哪些是最活跃、最具影响力的人?
在艾滋病等疾病传播网络中，哪些人是最危险的?
…

**介数中心性：**经过某个节点的最短路径的数目来刻画节点重要性的指标就称为介数中心性。

**紧密中心性：**如果节点到图中其他节点的最短距离都很小，那么它的接近中心性就很高。相比介数中心性，接近中心性更接近几何上的中心位置。

有关节点的性质，度中心性、介数中心性和紧密中心性都是常见的评价无向网络的重要指标，

在这放一个链接，方便同学们深入学习以上三个指标以及有向图的中心性求解算法：

(20条消息) 图或网络中的中心性：点度中心性、中介中心性、接近中心性、特征向量中心性、PageRank_不务正业的土豆的博客-CSDN博客_点度中心度

网络整体的性质：

连通性(Connectivity): 如果网络中任意一个点都能到达网络中所有的其他点，那么网络是连通的。

**密度：**指网络中实际存在的边数与最大可能边数之比：

\rho=\frac{M}{\frac{1}{2} N(N-1)}

其中，M代表网络中边的数量，N代表所有网络中的节点数；

**直径：**网络中任意两个节点之间最短距离的最大值。

对于小型网络而言，直径可计算，用来分析整个网络的稳定性。

对于较为复杂的网络而言，可以进行直径的估算。

贴一个申必链接：

复杂网络属性计算之直径和介数 (bourneli.github.io)

**平均路径长度：**任意两个节点之间距离的平均值。

由平均路径长度引出的小世界现象，有兴趣的话可以看看这个实例**：**

(20条消息) 小世界现象_weixin_34343308的博客-CSDN博客

**聚集系数：**节点周边实际的边数与应该存在的最多边数之间的比值。

$c=\frac{2 \mathrm{E}}{K(K-1)}$

计算方法和密度近似，因此不再赘述。

网络鲁棒性分析

了解了这些指标，我们如何对网络进行系统地分析呢？首先引入一个概念：

**鲁棒性：**鲁棒是Robust的音译，也就是健壮和强壮的意思。它也是在异常和危险情况下系统生存的能力。网络鲁棒性是指网络遭到随机故障或蓄意攻击时仍能维持其功能的能力.在网络中，如果缺失了一些节点或者边，是否对网络的性能有较大的影响？这是我们需要考虑的问题。

举例来说，我们日常使用的校园网，如果线路意外中断了，导致用户体验问题雪上加霜，当然是会被投诉的。这就要求在设计时有足够的考虑以及对突发情况的模拟。

衡量网络鲁棒性的指标选取:

中心性以及度；
图的连通性
网络生存性（network survivability），是指在网络发生故障后能尽快利用网络中空闲资源为受影响的业务重新选路，使业务继续进行，以减少因故障而造成的社会影响和经济上的损失，使网络维护一个可以接受的业务水平的能力。

在建模过程中，鲁棒性分析是十分必要的，如果你的模型在数据发生微小变化、或者参数发生微小变化时，无法正常工作，那么你的模型正确性就要打一个大大的问号了。

因此，针对网络鲁棒性的具体分析，我在附件里放了两篇论文：

复杂网络的鲁棒性与中心性指标的研究_陆靖桥

城市轨道交通网络特性与级联失效鲁棒性分析_杨景峰

这两篇论文都对复杂网络的鲁棒性进行了分析，第一篇着重介绍网络数据集构建的网络，分析了蓄意攻击对网络的影响。第二篇论文除了对地铁网络受到攻击时的鲁棒性分析，还有部分拓展，同学们按需选择一篇阅读即可。

实战训练

说了这么多，不练练手还是很难理解的。实战部分我选择了2020年美赛D题和2021年美赛D题。

首先咱们来看看2020年美赛D题，对照着O奖论文，我们来看一看他的行文思路是什么，这里我们只关注对于数据的处理以及如何构建传球网络。

(20条消息) 2020美赛F奖论文（一）：摘要、绪论和模型准备_頔潇的博客-CSDN博客_美赛论文

Firstly，根据图论，在球员之间建立传球网络，并建立单次传球的价值评价模型，用于评价两两球员间传球的配合程度，即传球网络的边权。建立在一定时间范围内所有参与比赛的N个球员的邻接矩阵，通过以M个点的子完全图边权之和为排序关键字找出若干组优秀的M元组合。同时建立基于时间尺度的价值模型，用于评价时间对传球效率的影响。

(20条消息) 2020美赛F奖论文（二）：传球网络模型（PNM）的建立和影响因子分析_頔潇的博客-CSDN博客_传球网络

考虑到传球的质量/意义；传球时面对的防守压力（这里都需要自己的定义）+ 手动赋权
直观地分析出传球默契的组合，包括双人组和三人组
以微积分、概率论为工具，传球频率为指标衡量动态表现
直观地分析出传球默契的组合，包括双人组和三人组
以微积分、概率论为工具，传球频率为指标衡量动态表现
没有过于花里胡哨的作图（比如画个足球场、画个球员、画个球），而是遵守学术论文作图的规范，每张图的出现必然是为了更直观地传达更大的信息量，节省读者的时间。

接着我们看看2021美赛D题：

2021美赛D题O奖论文中文版+超详解读 - 知乎 (zhihu.com)

In Task1：
首先，我们以各音乐家为节点，综合考虑时间跨度与流派跨度的因素计算音乐家之间的有向影响力作为权重，建立有向音乐影响网络。然后我们使用社会网络分析（SNA）对影响网络进行分析。计算网络中音乐人的点度中心性，并进一步使用PageRank修正的Eigenvector Centrality，对音乐人的音乐影响进行评价, Bob Dylan、The Rolling Stones、Chuck Berry、Elvis Presley拥有最高的影响力。我们还发现服从幂律分布，意味着影响者与追随者满足Pareto’s Principle，较少数的音乐家影响绝大多数音乐家。