每日一题整理——2023.5

2023.5.1

通知所有员工所需的时间

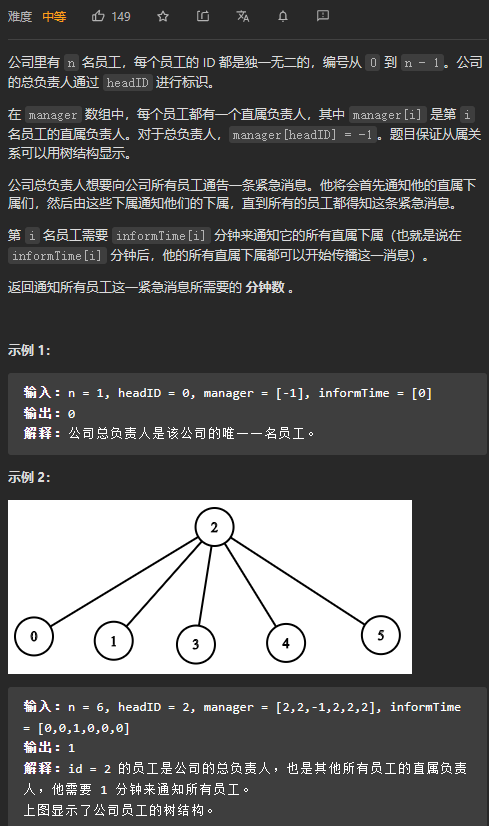
数据范围：

我的思路;

首先分析需要使用的数据结构，想到了使用树或者并查集作为基本的数据结构。但是后来发现并查集的话计算较为复杂，因此利用线性表构建了简单的树（搜索更加方便，感觉非线性的复杂度可能太高）。然后是对搜索方法的选择，dfs过了不到一半的用例，bfs倒是比较简单就通过了，不是很理解。

struct Node{
    int time;
    vector<int> next;
};
class Solution {
public:
    int numOfMinutes(int n, int headID, vector<int>& manager, vector<int>& informTime) {
        queue<Node> q;
        int result = informTime[0];
        const int maxn = 100001;
        Node node[maxn];
        for(int i = 0 ; i < n ; i++){
            node[i].time = informTime[i];
            if(manager[i] != -1){
                node[manager[i]].next.push_back(i);
            }
        }
        q.push(node[headID]);
        while(!q.empty()){
            int nn = q.size();
            while(nn--){
                Node temp = q.front();
                q.pop();
                for(int i = 0 ; i < temp.next.size() ; i++){
                    int tmp = temp.next[i];
                    node[tmp].time += temp.time;
                    result = max(node[tmp].time , result);
                    q.push(node[tmp]);
                }
            }
        }
        return result;
    }
};

2023.5.3

Find the Difference of Two Arrays

数据范围：

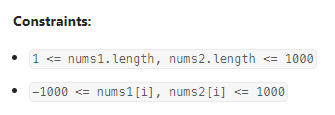
我的思路：

set去重，然后遍历find就结束了，还好数据范围不是很大。

class Solution {
public:
    vector<vector<int>> findDifference(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        unordered_set<int> s1;
        unordered_set<int> s2;
        for(int i = 0 ; i < m ;  i++){
            s1.insert(nums1[i]);
        }
        for(int i = 0 ; i < n ;  i++){
            s2.insert(nums2[i]);
        }
        vector<vector<int>> res;
        vector<int> res1;
        vector<int> res2;
        for(auto it = s1.begin() ; it!=s1.end() ; it++){
            if(s2.find(*it) == s2.end()){
                res1.push_back(*it);
            }
        }
        for(auto it = s2.begin() ; it!=s2.end() ; it++){
            if(s1.find(*it) == s1.end()){
                res2.push_back(*it);
            }
        }
        res.push_back(res1);
        res.push_back(res2);
        return res;
    }
};

2023.5.3

检查替换后的词是否有效

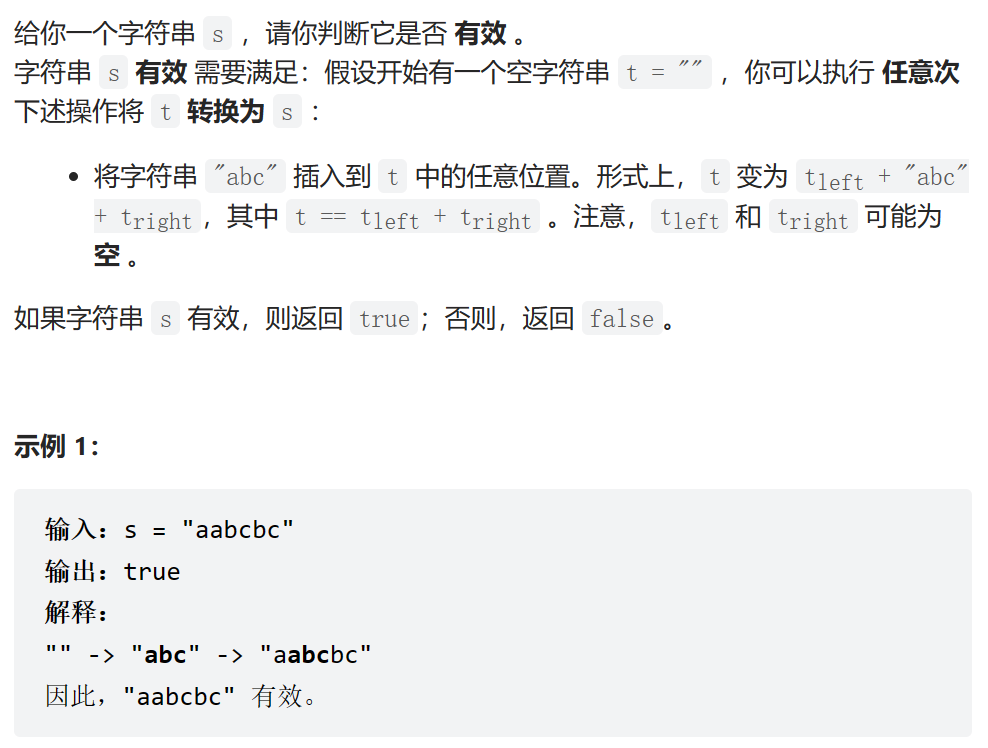
数据范围：

我的思路：

构建栈，对于成对的进行排除，最后判断栈空；

class Solution {
public:
    bool isValid(string s) {
        stack<char> ss;
        int n = s.length();
        for(int index = 0 ; index < n ; index++){
            if(s[index] == 'a'){
                ss.push('a');
            }
            else if(s[index] == 'b'){
                ss.push('b');
            }
            else if(s[index] == 'c'){
                if(ss.size() > 1 && ss.top() == 'b'){
                    char tmp1 = ss.top();
                    ss.pop();
                    char tmp2 = ss.top();
                    ss.pop();
                    if(tmp2 != 'a'){
                        ss.push(tmp2);
                        ss.push(tmp1);
                        ss.push('c');
                    }
                }
                else{
                    ss.push('c');
                }
            }
        }
        if(ss.empty()){
            return true;
        }
        return false;
    }
};

2023.5.5

Maximum Number of Vowels in a Substring of Given Length

数据范围：

我的思路：

按理来说这道题十分钟就能写完，但是我由于看题太粗心以为直接求最长元音字母串就完事了，后来发现是求所有的子串中元音最多，这里就用了简单的数组记忆了前缀元音和，然后差值比较就完事了。

class Solution {
public:
    int maxVowels(string s, int k) {
        int len = s.length();
        char a[5] = {'a','e','i','o','u'};
        vector<int> dp(len,0);
        for(int i = 0 ; i < 5 ; ++i){
            if(s[0] == a[i]){
                dp[0] = 1;
                break;
            }
        }
        for(int i = 1 ; i < len ; ++i){
            int j;
            for(j = 0 ; j < 5 ; ++j){
                if(a[j] == s[i]){
                    break;
                }
            }
            if(j == 5){
                dp[i] = dp[i-1];
            }
            else{
                dp[i] = dp[i-1] + 1;
            }
        }
        int max_len = dp[k-1];
        for(int i = k ; i < len ; ++i){
            max_len = max(max_len , dp[i] - dp[i-k]);
            if(max_len > k){
                max_len = k;
                break;
            }
        }
        return max_len;
    }
};

2023.5.5

处理用时最长的那个任务的员工

数据范围：

我的思路：

数据范围小，我直接重拳出击！

class Solution {
public:
    int hardestWorker(int n, vector<vector<int>>& logs) {
        int index = logs[0][0];
        int max_value = logs[0][1];
        int len = logs.size();
        for(int i = 1 ; i < len ; i++){
            int temp = logs[i][1] - logs[i-1][1];
            if(temp > max_value){
                max_value = temp;
                index = logs[i][0];
            }
            else if(temp == max_value){
                index = min(index , logs[i][0]);
            }
        }
        return index;
    }
};

2023.5.6

数青蛙

数据范围：

我的思路：

试过许多方法：栈存、队列或者深搜，发现都不如这暴力来的爽，故此记录一下。栈存的话，也需要对这五个字母进行计数，判断，不如直接一遍过。代码如下：

class Solution {
public:
    int minNumberOfFrogs(string croakOfFrogs) {
        int len = croakOfFrogs.length();
        int c=0,r=0,o=0,a=0,k=0;
        int res = 0;
        for(int i = 0 ; i < len ; i++){
            if(croakOfFrogs[i] == 'c'){
                c++;
            }
            else if(croakOfFrogs[i] == 'r'){
                r++;
            }
            else if(croakOfFrogs[i] == 'o'){
                o++;
            }
            else if(croakOfFrogs[i] == 'a'){
                a++;
            }
            else{
                k++;
            }
            res = max(c-k,res);
            if(c < r || r < o || o < a || a < k ){
                return -1;
            }
        }
        if(c == r && r == o && o == a && a == k){
            return res;
        }
        return -1;
    }
};

2023.5.6

Number of Subsequences That Satisfy the Given Sum Condition

数据范围：

我的思路：

这里我利用数组进行2的次幂存储，然后从序列的两边进行遍历，找到两端之和小于目标值的，然后对两个数字中间包含的数字进行求解子集的数量。代码如下：

class Solution {
public:
    int numSubseq(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int res = 0, n = nums.size(), l = 0, r = n - 1, mod = 1e9 + 7;
        vector<int> pows(n, 1);
        for (int i = 1 ; i < n ; ++i)
            pows[i] = pows[i - 1] * 2 % mod;
        while (l <= r) {
            if (nums[l] + nums[r] > target) {
                r--;
            } else {
                res = (res + pows[r - l++]) % mod;
            }
        }
        return res;
    }
};

2023.5.7

Find the Longest Valid Obstacle Course at Each Position

数据范围：

我的思路：

第一次看的时候，以为只需要利用数组存储每一段的最长字段，然后遍历一遍就行，结果发现同高度有限制，不能视为一致的个体。接着就在遍历的过程中考虑了当前端点在之前出现过这种情况，发现这样会超时。最终换了一种思考方式：

构建一个一维数组，其中下标代表出现的顺序，元素代表出现的元素。对于每一个遍历到的元素，判断是否大于其中的某个值，找到第一个大于的值之后返回。为什么是第一个呢？其实，这个一维数组的顺序是递增的，这里很巧妙地避免了后续元素的遍历问题，节省了计算量。找到目标值后，用当前的值进行替换，而后进行次数的计算。代码如下：

class Solution {
public:
    vector<int> longestObstacleCourseAtEachPosition(vector<int>& obstacles) {
        int n = obstacles.size();
        vector<int> v;
        vector<int> dp(n,1);
        for(int i = 0 ; i < n ; i++){
            int j = upper_bound(v.begin(), v.end(), obstacles[i]) - v.begin();
            if(j == v.size()){
                v.push_back(obstacles[i]);
            }
            else{
                v[j] = obstacles[i];
            }
            dp[i] = j + 1;
        }
        return dp;
    }
};

2023.5.10

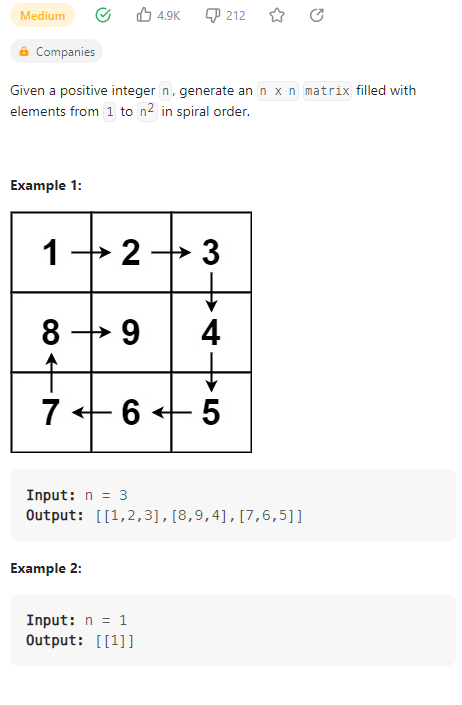
Spiral Matrix II

数据范围：

我的思路：

什么easy题，这不是有手就行？虽然昨天做了道类似的边界条件调了十五分钟。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n,vector<int>(n));
        int index = 1;
        for(int i = 0 ; i < n ; i++){
            for(int j = i ; j < n-i ; j++){
                res[i][j] = index++;
            }
            for(int j = i+1 ; j < n-i-1 ; j++){
                res[j][n-i-1] = index++;
            }
            for(int j = n-i-1 ; j >= i && n-i-1 != i; j--){
                res[n-i-1][j] = index++;
            }
            for(int j = n-i-2 ; j > i && n-i-2 != i; j--){
                res[j][i] = index++;
            }
        }
        return res;
    }
};

2023.5.10

可被 K 整除的最小整数

数据范围：

我的思路：

可以构建递归式，即：

$$K(N) = (K(N-1)\%k \times 10+1)\%k$$

其中K(N)代表长度为N的11数字序列，因此每次将被除数缩短即可；

class Solution {
public:
    int smallestRepunitDivByK(int k) {
        if(k%2 == 0 || k%5 == 0){
            return -1;
        }
        int i = 1;
        for(int n = 1 ; n%k != 0 ; i++){
            n %= k;
            n = n * 10 + 1;
        }
        return i;
    }
};

2023.5.11

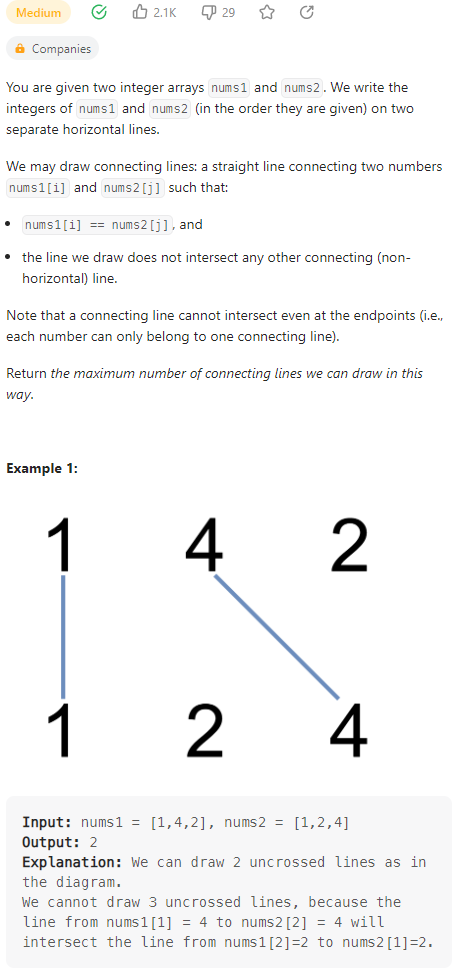
Uncrossed Lines

数据范围：

我的思路：

第一眼觉得应该是dp，所以就试着构造了一下，公式如下：

$$dp[i][j]=dp[i-1][j-1]+1\quad (s1[i]==s2[j])$$

$$dp[i][j] = max(dp[i-1][j],dp[i][j-1]) \quad (s1[i]!=s2[j])$$

其中，dp[i][j]代表s1[0-i]和s2[0-j]对应的最佳匹配数量。首先对第一行和第一列的dp数组进行初始化，初始化后对其他部分进行处理，对于出现最佳匹配的点，我们考虑利用恰好不包含两个元素的序列的历史状态处理，对于未出现最佳匹配的序列，进行前一个历史状态的替换。需要注意的是，第一次考虑的时候我将dp[i-1][j-1]也放进了不相等的情况中考虑，这个是完全没有必要的，因为必然存在dp[i-1][j]和dp[i][j-1]≥dp[i-1][j-1]，因此最终的代码如下：

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int index_1 = 0;
        int index_2 = 0;
        int len1 = nums1.size();
        int len2 = nums2.size();
        vector<vector<int>> dp(len1,vector<int>(len2,0));
        dp[0][0] = nums1[0] == nums2[0] ? 1:0;
        for(int i = 1 ; i < len2 ; i++){
            if(nums1[0] == nums2[i]){
                dp[0][i] = 1;
            }
            else{
                dp[0][i] = dp[0][i-1];
            }
        }
        for(int i = 1 ; i < len1 ; i++){
            if(nums2[0] == nums1[i]){
                dp[i][0] = 1;
            }
            else{
                dp[i][0] = dp[i-1][0];
            }
        }
        for(int i = 1 ; i < len1 ; i++){
            for(int j = 1 ; j < len2 ; j++){
                if(nums1[i] == nums2[j]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[len1-1][len2-1];
    }
};

2023.5.11

子串能表示从 1 到 N 数字的二进制串

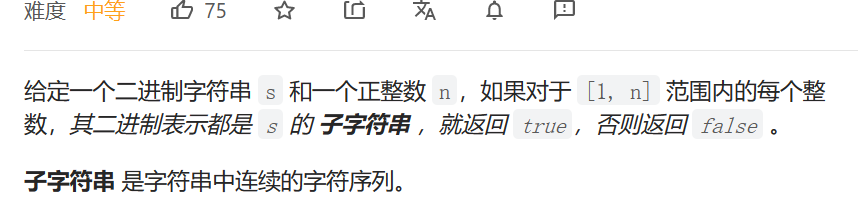
数据范围：

我的思路：

ee，暴力求解把；

class Solution {
public:
    bool queryString(string s, int n) {
        for(int i = 1 ; i <= n ; i++){
            int temp = i;
            string s1="";
            int tmp;
            while(temp){
                tmp = temp&1;
                s1 += (tmp+'0');
                temp >>= 1;
            }
            reverse(s1.begin(),s1.end());
            if(s.find(s1) == -1){
                return false;
            }
        }
        return true;
    }
};

2023.5.12

翻转子数组得到最大的数组值

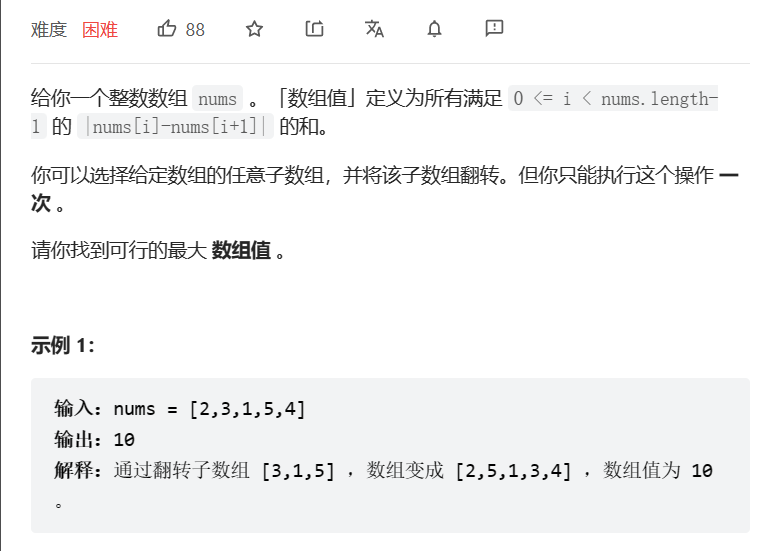
数据范围：

我的思路：

分类讨论，子数组的翻转只会对两端的差值产生影响，因此我们只需要对子数组的两个端点进行分析即可。对于端点在最左端、最右端的情况是最容易解决的，但是对于子数组两端都在内部的情况，还需要进行深入的讨论。具体的讨论过程可以参考力扣的官方解法：

通过上述的讨论可以得到最终的递推式：

class Solution {
public:
    int maxValueAfterReverse(vector<int>& nums) {
        int value = 0, n = nums.size();
        for(int i = 0 ; i < n-1 ; i++){
            value += abs(nums[i]-nums[i+1]);
        }
        int mx1 = 0;
        for(int i = 1 ; i < n-1 ; i++){
            mx1 = max(mx1,abs(nums[0]-nums[i+1])-abs(nums[i]-nums[i+1]));
            mx1 = max(mx1,abs(nums[n-1]-nums[i-1])-abs(nums[i]-nums[i-1]));
        }
        int mx2 = INT_MIN;
        int mn2 = INT_MAX;
        for(int i = 0 ; i < n-1 ; i++){
            int x = nums[i];
            int y = nums[i+1];
            mx2 = max(mx2,min(x,y));
            mn2=  min(mn2,max(x,y));
        }
        return value+max(mx1,2*(mx2-mn2));
    }
};

2023.5.12

Solving Questions With Brainpower

数据范围：

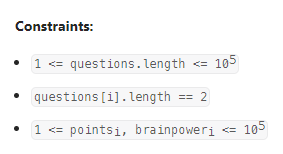
我的思路：

这道题唯一的最优点是能想到动态规划，但是动态规划的遍历方向错了。这里的错误点就是在最后结束处是应当最先初始化的。递推的公式如下：

$$dp[i] = max(dp[i+1],questions[i][0]+dp[min(n,questions[i][1]+i+1)])$$

具体的代码如下：

class Solution {
public:
    long long mostPoints(vector<vector<int>>& questions) {
        int n = questions.size();                              
        vector<long long> dp(n+1,0);
        for(int i = n-1 ; i >= 0 ; i--){
            int points = questions[i][0];
            int jump = questions[i][1];

            jump = min(n,jump+i+1);
            long long temp = points + dp[jump];
            dp[i] = max(dp[i+1],temp);
        }
        return dp[0];
    }
};

2023.5.13

与对应负数同时存在的最大正整数

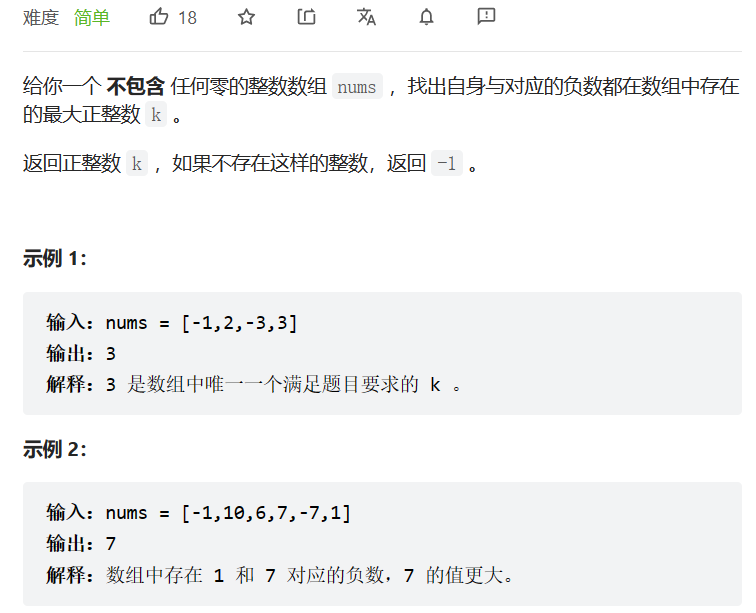
数据范围：

我的思路：

sort排序+双指针。

class Solution {
public:
    int findMaxK(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin() , nums.end());
        int left = 0;
        int right = n-1;
        while(left < right){
            if(nums[left] + nums[right] > 0){
                right--;
            }
            else if(nums[left] + nums[right] < 0){
                left++;
            }
            else{
                return nums[right];
            }
        }
        return -1;
    }
};

2023.5.13

Count Ways To Build Good Strings

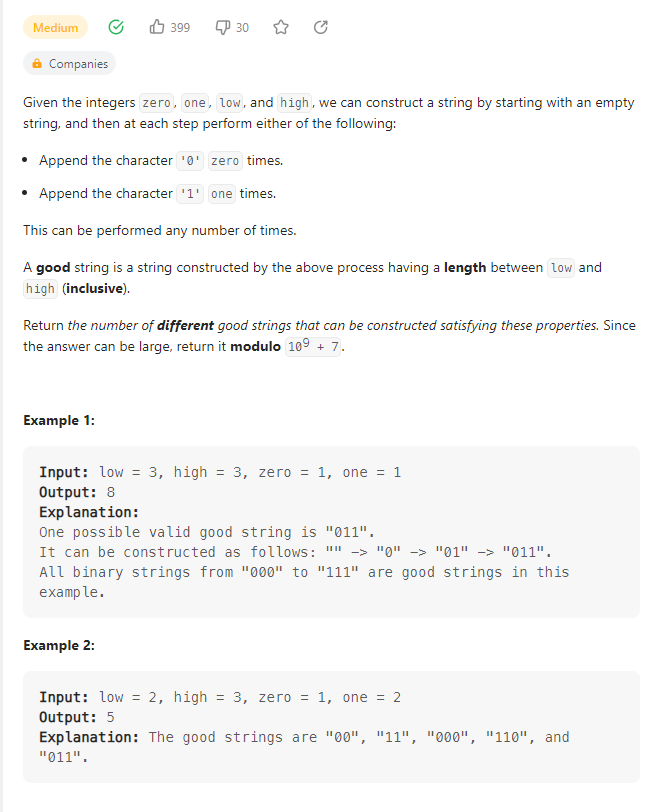
数据范围：

我的思路：

第一次用dfs，果然爆了。第二次一看，这不是爬楼梯那个简单dp吗？感觉思路错了就很难纠正回来。最后初始化废了一些时间。

class Solution {
public:
    int countGoodStrings(int low, int high, int zero, int one) {
        vector<int> dp(high+1,0);
        const int mod = 1000000007;
        int res = 0;
        int index_1 = min(zero,one);
        int index_2 = max(zero,one);
        for(int i = index_1  ; i <= index_2 ; i+=index_1){
            dp[i]++;
        }
        dp[index_2]++;
        for(int i = index_2+1 ; i <= high ; i++){
            dp[i] = (dp[i-zero] + dp[i-one])%mod;
        }
        for(int i = low ; i <= high ; i++){
            res = (res + dp[i])%mod;
        }
        return res;
    }
};

2023.5.14

Maximize Score After N Operations

数据范围：

我的思路：

枚举，因为整体的范围并不是很大，但是我发现枚举会爆掉，从题解中了解到可以使用掩码来区分是否产生了重叠，从而大幅度优化枚举的过程。

class Solution {
public:
    int dp[8][16384] = {};
    int maxScore(vector<int>& n, int i = 1, int mask = 0) {
        if (i > n.size() / 2)
            return 0;
        if (!dp[i][mask])
            for (int j = 0; j < n.size(); ++j)
                for (auto k = j + 1; k < n.size(); ++k) {
                    int new_mask = (1 << j) + (1 << k);
                    if ((mask & new_mask) == 0)
                        dp[i][mask] = max(dp[i][mask], i * __gcd(n[j], n[k]) + maxScore(n, i + 1, mask + new_mask));
                }
        return dp[i][mask];
    }
};

2023.5.14

距离相等的条形码

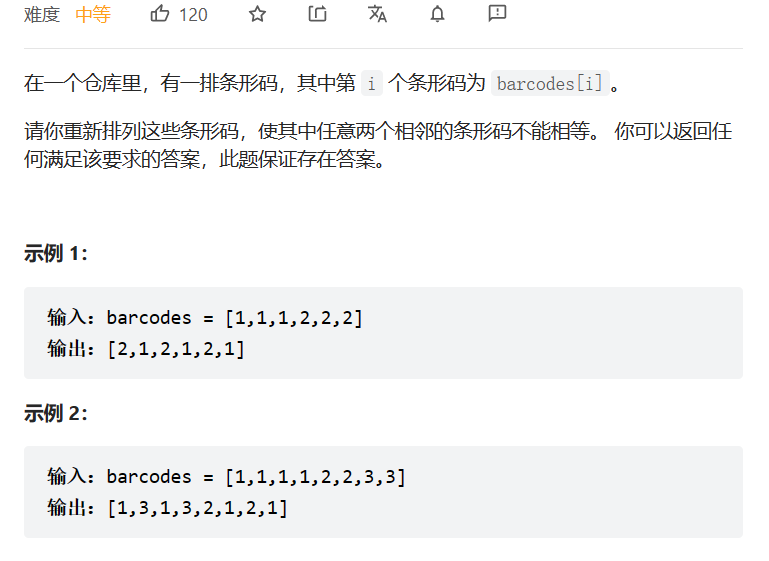
数据范围：

我的思路：

开始想用双指针直接做，对于中间部分连续较长的部分进行已有vector的插入，但是后来发现数组越界了，为了防止陷入到持续进行分类讨论的泥潭中，我觉得还是得恩造stl，首先记录各个数字的数量，然后将对应的pair压入优先队列，每次取出现次数最多的两个元素构成两位，以此类推，最终获得不相邻的数组。

class Solution {
public:
    vector<int> rearrangeBarcodes(vector<int>& barcodes) {
        int n = barcodes.size();
        vector<int> res;
        if(n == 1){
            return barcodes;
        }
        unordered_map<int,int> mp;
        for(int i = 0 ; i < n ; i++){
            if(mp.find(barcodes[i]) == mp.end()){
                mp[barcodes[i]] = 1;
            }
            else{
                mp[barcodes[i]]++;
            }
        }
        priority_queue<pair<int ,int>> q;
        for(auto it = mp.begin() ; it !=mp.end() ; it++){
            q.push(make_pair(it->second , it->first));
        }
        while(q.size() > 1){
            pair<int , int> p1 = q.top();
            q.pop();
            pair<int , int> p2 = q.top();
            q.pop();
            res.push_back(p1.second);
            p1.first--;
            res.push_back(p2.second);
            p2.first--;
            if(p1.first > 0){
                q.push(p1);
            }
            if(p2.first > 0){
                q.push(p2);
            }
        }
        if(!q.empty()){
            res.push_back(q.top().second);
        }
        return res;
    }
};

2023.5.15

Swapping Nodes in a Linked List

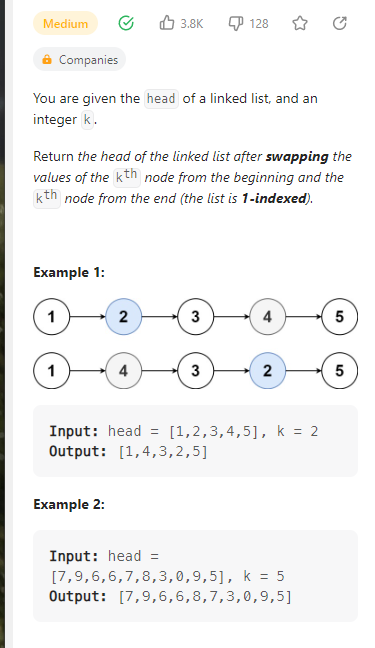
数据范围：

我的思路：

首先是用队列储存确定数量，然后依次出列确定交换位置。这里没有使用双指针，确实是我的失误。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapNodes(ListNode* head, int k) {
        queue<ListNode*> q;
        ListNode* h = head;
        while(h){
            q.push(h);
            h = h->next;
        }
        h = head;
        int n = q.size();
        int left = min(k,n-k+1);
        int right = max(k,n-k+1);
        if(left == right){
            return head;
        }
        ListNode* ll = NULL;
        ListNode* rr = NULL;
        ListNode* pre_1;
        ListNode* pre_2;
        ListNode* pre = NULL;
        ListNode* temp;
        int index = 1;
        while(!ll || !rr){
            temp = q.front();
            if(index == left){
                ll = temp;
                pre_1 = pre;
            }
            else if(index == right){
                rr = temp;
                pre_2 = pre;
            }
            pre = temp;
            q.pop();
            index++;
        }

        if(left == 1){
            pre_2->next = ll;
            rr->next = ll->next;
            ll->next = NULL;
            head = rr;
        }
        else{
            pre_2->next = ll;
            temp = ll->next;
            ll->next = rr->next;
            pre_1->next = rr;
            rr->next = temp;
        }
        return head;
    }
};

然后是使用双指针做的，这里先找到左端点位置，在分别从起点和左端点出发，跨越n-k个节点到达倒数第k个节点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapNodes(ListNode* head, int k) {
        ListNode* left = head;
        ListNode* right = head;

        for(int i = 1 ; i < k ; i++){
            left = left->next;
        }

        ListNode* l = left;
        while(l->next!=NULL){
            right = right->next;
            l = l->next;
        }

        int temp = left->val;
        left->val = right->val;
        right->val = temp;
        return head;
    }
};

2023.5.15

按列翻转得到最大值等行数

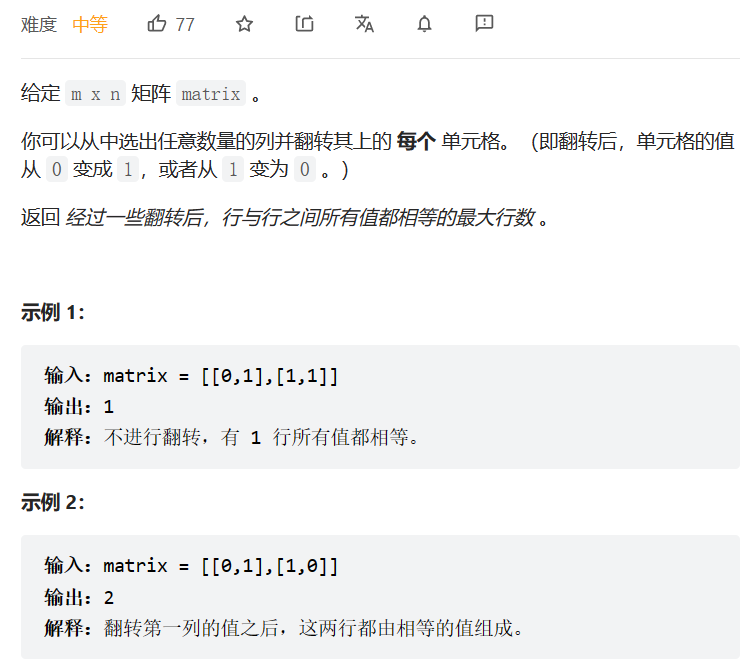
数据范围：

我的思路：

最开始的思路是利用动态规划+深搜（其实本质上我觉得就是深搜），对于前i个元素而言，判断存在的各元素相等的字符串个数，如果出现了数量减少的情况，就对末尾元素进行翻转操作，然后计算两种情况的最大值，依次递归。后来发现结果爆了。后来发现哈希不错，只需要记录该模式串和逆模式串的数量，然后获取最大的模式串数量即可。最终的代码如下：

class Solution {
public:
    int maxEqualRowsAfterFlips(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int result = 0;
        unordered_map<string , int> mp;
        string s1 = string('0',n);
        string s2 = string('1',n);
        for(int i = 0 ; i < m ; i++){
            string temp;
            string tmp;
            for(int j = 0 ; j < n ; j++){
                temp += (matrix[i][j]+'0');
                int t = matrix[i][j] == 0 ? 1 : 0;
                tmp += (t + '0');
            }
            mp[temp]++;
            mp[tmp]++;
        }
        for(auto it = mp.begin() ; it != mp.end() ; it++){
            result = max(it->second , result);
        }
        return result;
    }
};

2023.5.16

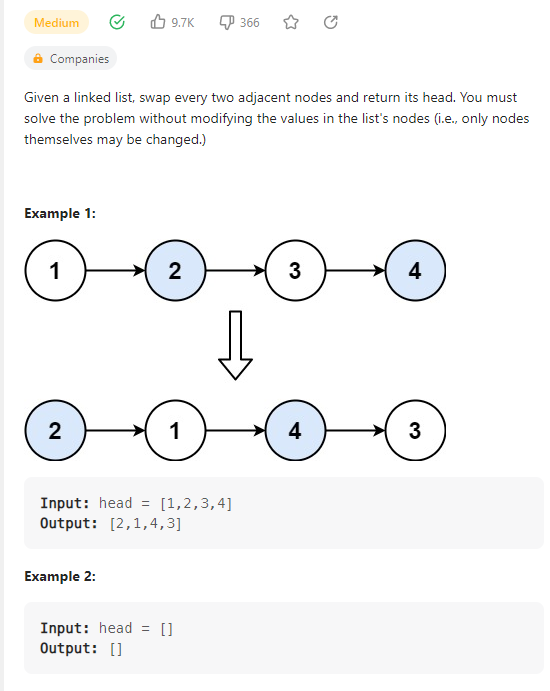
Swap Nodes in Pairs

数据范围：

我的思路：

第一种思路，就是构建队列存储，每次对前两个元素进行交换，本质上就是对整个进行一次遍历，没什么价值，差点就超时了

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        queue<ListNode*> q;
        if(head == NULL || head->next == NULL){
            return head;
        }
        ListNode* h = head->next;
        head->next = h->next;
        h->next = head;
        ListNode* p = h;
        ListNode* pre = head;
        h = pre->next;
        while(h){
            q.push(h);
            h = h->next;
        }
        while(q.size() > 1){
            ListNode* t1 = q.front();
            q.pop();
            ListNode* t2 = q.front();
            q.pop();
            t1->next = t2->next;
            t2->next = t1;
            pre->next = t2;
            pre = pre->next->next;
        }
        if(!q.empty()){
            pre->next = q.front();
        }
        return p;
    }
};

第二种思路，就是直接构建前驱节点和当前节点，也不是很复杂。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head == NULL || head->next == NULL){
            return head;
        }
        ListNode* pre = new ListNode();
        ListNode* cur = head;
        ListNode* h = pre;
        while(cur && cur->next){
            pre->next = cur->next;
            cur->next = pre->next->next;
            pre->next->next = cur;

            pre = cur;
            cur = cur->next;
        }
        return h->next;
    }
};

2023.5.16

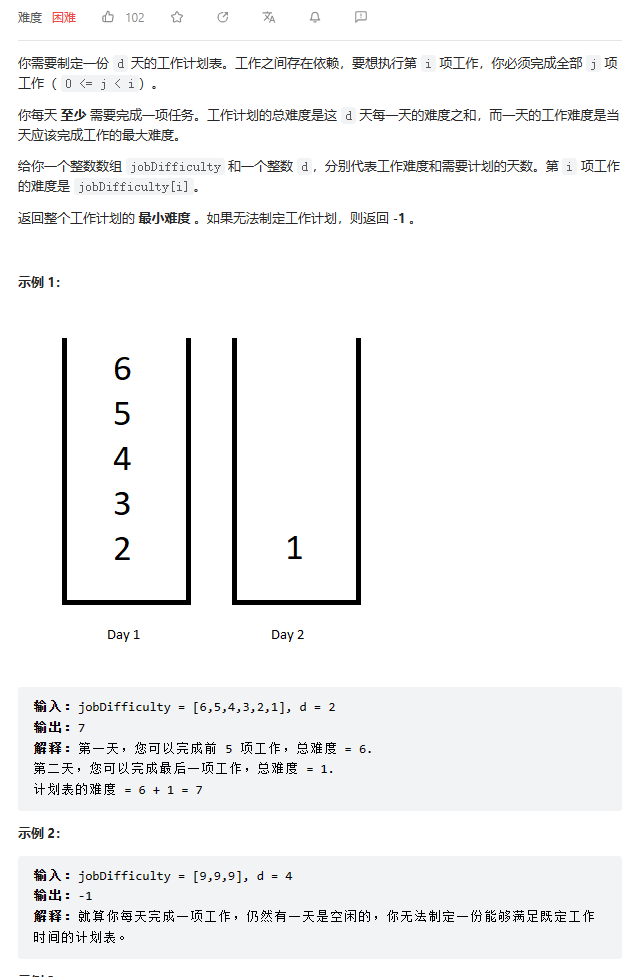
工作计划的最低难度

数据范围：

我的思路：

题干翻译成人话意思就是根据给出的区间数，求解所有区间最大值和最小的情况。这里果断想到了dp，但是具体的实现和答案不太一样。我想做的是第i天到第j天的最大值，然后根据这个求和，但是这样明显过于复杂了，因此考虑使用如下的情况：

$$dp[i][j] = min(dp[i][j] , dp[i-1][k-1] + f(k,j))$$

这里，dp[i][j]代表到第i天总共完成了j项任务，f(k,j)代表完成第k项任务到第j项任务需要花费的时间。总的来说，就是将每一天的总任务选取内部点进行划分，每次计算最小的最大值，最终得到结果：

class Solution {
public:
    int minDifficulty(vector<int>& jobDifficulty, int d) {
        int n = jobDifficulty.size();
        if(d > n){
            return -1;
        }

        const int INF = 1000000007;
        vector<vector<int>> dp(n+1,vector<int>(n+1,INF));
        int ma = 0;
        for(int i = 0 ; i < n ; i++){
            ma = max(jobDifficulty[i],ma);
            dp[0][i] = ma;
        }

        for(int i = 1 ; i < d ; i++){
            for(int j = 1 ; j < n ; j++){
                ma = 0;
                for(int k = j ; k>= i ; k--){
                    ma = max(ma,jobDifficulty[k]);
                    dp[i][j] = min(dp[i][j] , dp[i-1][k-1]+ma);
                }
            }
        }

        return dp[d-1][n-1];
    }
};

2023.5.17

判断两个事件是否存在冲突

数据范围：

我的思路：

不存在跨天问题，直接转成时间戳比较就行。

class Solution {
public:
    bool haveConflict(vector<string>& event1, vector<string>& event2) {
        int h;
        int m;
        vector<int> minute(4);
        for(int i = 0 ; i < 2 ; i++){
            minute[i] = ((event1[i][0]-'0')*10 + (event1[i][1]-'0'))*60+(event1[i][3]-'0')*10 + (event1[i][4]-'0');
        }
        for(int i = 0 ; i < 2 ; i++){
            minute[i+2] = ((event2[i][0]-'0')*10 + (event2[i][1]-'0'))*60+(event2[i][3]-'0')*10 + (event2[i][4]-'0');
        }
        if(minute[1] < minute[2] || minute[3] < minute[0]){
            return false;
        }
        return true;
    }
};

2023.5.17

Maximum Twin Sum of a Linked List

数据范围：

我的思路：

第一次用昨天的双指针套路构建了一个ON^2的算法，超时了。然后将搜索的范围缩小了，还是超时了。最后直接将之前遍历过的节点用栈进行存储，在中间之后进行求和，复杂度ON。最后看题解发现是对于左半部分节点全部两两互换位置，然后在进行双指针求和，感觉和我的也没差多少，我的也就存储空间差了点。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    int pairSum(ListNode* head) {
        ListNode* left = head;
        ListNode* right = head;
        stack<ListNode*> s;
        while(right){
            s.push(left);
            left = left->next;
            right = right->next->next;
        }
        int max_value = 0;
        while(!s.empty()){
            ListNode *h = s.top();
            s.pop();
            max_value = max(max_value , h->val+left->val);
            left = left->next;
        }
        return max_value;
    }
};

`

2023.5.18

负二进制数相加

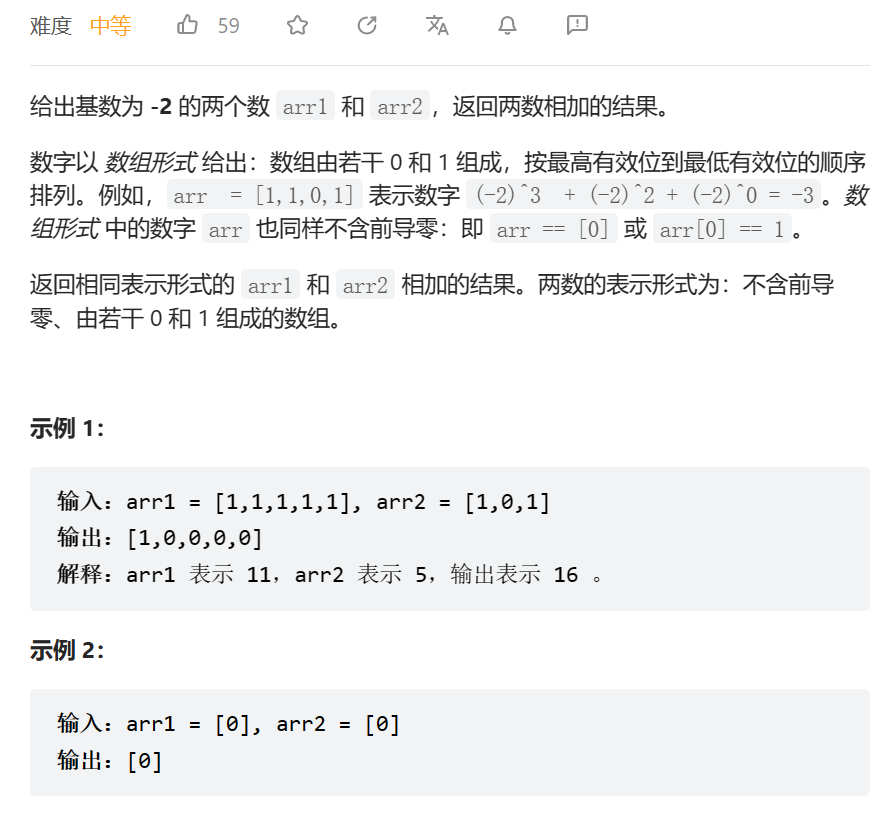
数据范围：

我的思路：

高精度加法的模拟，注意进位和普通二进制加法的差异即可。

class Solution {
public:
    vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
        int i = arr1.size() - 1, j = arr2.size() - 1;
        vector<int> ans;
        for (int c = 0; i >= 0 || j >= 0 || c; --i, --j) {
            int a = i < 0 ? 0 : arr1[i];
            int b = j < 0 ? 0 : arr2[j];
            int x = a + b + c;
            c = 0;
            if (x >= 2) {
                x -= 2;
                c -= 1;
            } else if (x == -1) {
                x = 1;
                c += 1;
            }
            ans.push_back(x);
        }
        while (ans.size() > 1 && ans.back() == 0) {
            ans.pop_back();
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

2023.5.18

Minimum Number of Vertices to Reach All Nodes

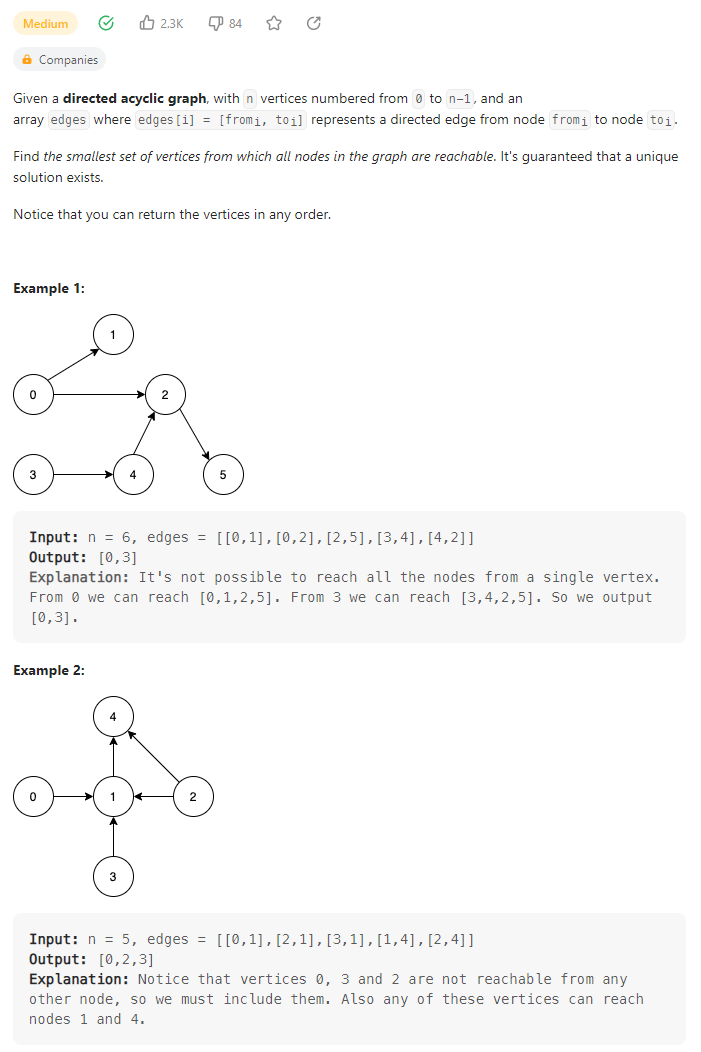
数据范围：

我的思路：

求并查集，即计算每个连通图的起点（即起始节点）。

class Solution {
public:
    int findfather(vector<int>& father , int index){
        if(father[index] == index){
            return index;
        }
        return father[index] = findfather(father,father[index]);
    }
    vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {
        int m = edges.size();
        vector<int> father(n);
        vector<int> res;
        for(int i = 0 ; i < n ; ++i){
            father[i] = i;
        }
        for(int i = 0 ; i < m ; i++){
            int a = edges[i][0];
            int b = edges[i][1];
            int fa = findfather(father,a);
            if(fa!=father[b]){
                father[b] = fa;
            }
        }
        unordered_set<int> ss;
        for(int i = 0 ; i < n ; i++){
            if(father[i] == i){
                res.push_back(i);
            }
        }
        return res;
    }
};

2023.5.19

活字印刷

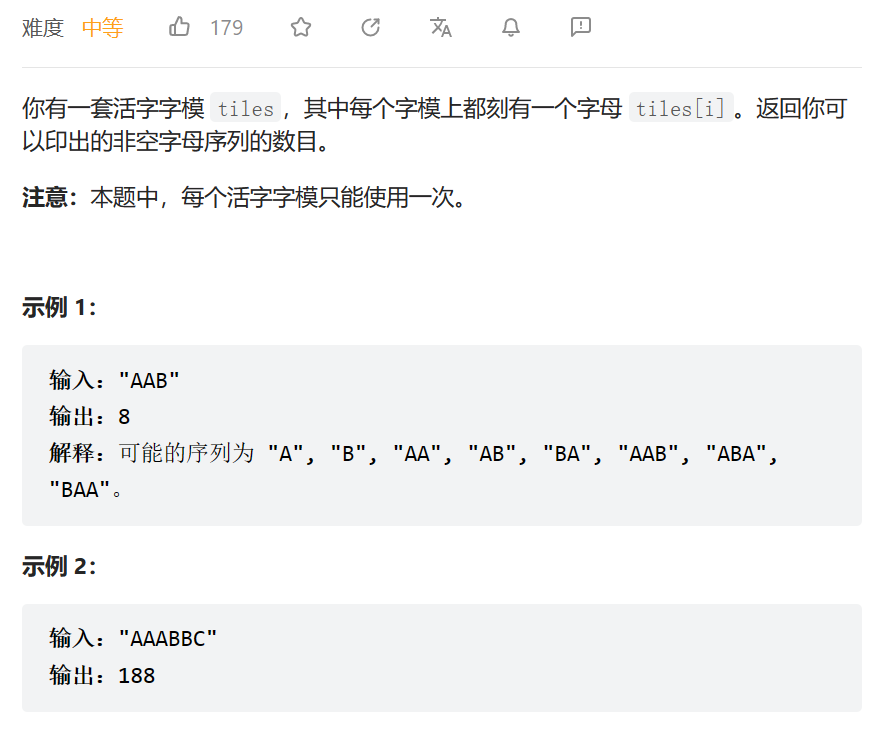
数据范围：

我的思路：

这题的数据范围比较小，因此直接dfs回溯即可。

class Solution {
public:
    unordered_set<string> hash;
    void dfs(string &tiles, string &s, vector<bool>& v){
        hash.insert(s);
        if(s.length() == tiles.length()){
            return ;
        }
        for(int i = 0 ; i < tiles.length() ; ++i){
            if(!v[i]){
                v[i] = true;
                s += tiles[i];
                dfs(tiles, s, v);
                s.pop_back();
                v[i] = false;
            }
        }
    }
    int numTilePossibilities(string tiles) {
        int len = tiles.length();
        string s;
        vector<bool> v(len,false);
        dfs(tiles,s,v);
        return hash.size()-1;
    }
};

2023.3.19

Is Graph Bipartite?

数据范围：

我的思路：

之前没做过这样的题，因此对二分图的判断这里需要着重说明一下。首先，什么是二分图？简单来说，二分图就是将图的点集划分成两个部分，对于边集而言，任意一条边的顶点分别存在于两个点集中。这道题需要对图形进行二分图判断，这里使用颜色标记法进行处理，其核心思想为对于部分边集中的所有点，没有边相连，因此可以从任意顶点出发，对当前节点和相邻结点进行不同的标色处理。如果存在相邻两点颜色相同，证明该图不是二分图。具体的代码如下：

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<int> q;
        vector<int> color(n,0);
        for(int i = 0 ; i < n ; i++){
            if(color[i]){
                continue;
            }
            color[i] = 1;
            q.push(i);
            while(!q.empty()){
                int temp = q.front();
                int nn = graph[temp].size();
                for(int j = 0 ; j < nn ; j++){
                    if(!color[graph[temp][j]]){
                        color[graph[temp][j]] = -color[temp];
                        q.push(graph[temp][j]);
                    }
                    else if(color[graph[temp][j]] == color[temp]){
                        return false;
                    }
                }
                q.pop();
            }
        }
        return true;
    }
};

2023.5.20

Evaluate Division

数据范围：

我的思路：

额，感觉我写的有一点点复杂。首先对等式数组进行遍历，对每一对字符串进行操作：

• 判断之前是否出现过，如果出现过直接在先前的树节点上添加连接节点；如果没有出现过，则添加新的节点；
• 在添加节点的过程中，注意去重问题；

然后对每一个查询进行遍历，对于每一个搜索对，因为之前的邻接信息存储时双向的，因此可以直接使用dfs对每一个查询对的第一个字符串进行搜索，在搜索过程中保证无环，最终获得最优解。

struct Node{
    string name;
    int ii;
    unordered_map<int,double> next;
};
class Solution {
public:
    Node node[40];
    bool v[40];
    double dfs(int j, int k, int now){
        for(auto it = node[now].next.begin() ; it != node[now].next.end() ; it++){
            if(!v[it->first]){
                if(it->first == k){
                    return it->second;
                }
                v[it->first] = true;
                double temp = dfs(j,k,it->first);
                if(temp!=-1){
                    return temp*it->second;
                }
            }
        }
        return -1.0;
    }
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        int n = equations.size();
        int m = queries.size();
        int index = 0;

        for(int i = 0 ; i < n ; ++i){
            string s1 = equations[i][0];
            string s2 = equations[i][1];
            int index_1;
            int index_2;

            for(index_1 = 0 ; index_1 < index ; ++index_1){
                if(node[index_1].name == s1){
                    break;
                }
            }

            for(index_2 = 0 ; index_2 < index ; ++index_2){
                if(node[index_2].name == s2){
                    break;
                }
            }

            if(index_1 == index && index_2 == index){
                node[index].name = s1;
                node[index].ii = index;
                node[index].next[index+1] = values[i];
                ++index;
                node[index].name = s2;
                node[index].ii = index;
                node[index].next[index-1] = 1.0/values[i];
                ++index;
            }
            else if(index_1 == index){
                node[index].name = s1;
                node[index].ii = index;
                node[index].next[index_2] = values[i];
                node[index_2].next[index] = 1.0/values[i];
                ++index;
            }
            else if(index_2 == index){
                node[index].name = s2;
                node[index].ii = index;
                node[index].next[index_1] = 1.0/values[i];
                node[index_1].next[index] = values[i];
                ++index;
            }
            else{
                node[index_1].next[index_2] = values[i];
                node[index_2].next[index_1] = 1.0/values[i];
            }
        }

        // cout<<index<<endl;
        // for(int i = 0 ; i < index ; i++){
        //     cout<<node[i].name << " "<< node[i].ii<<" ";
        //     for(auto it = node[i].next.begin() ; it!=node[i].next.end() ; it++){
        //         cout<<it->first<<" "<<it->second<<" ";
        //     }
        //     cout<<endl;
        // }

        vector<double> res;
        for(int i = 0 ; i < m ; ++i){
            string a = queries[i][0];
            string b = queries[i][1];
            int j,k;
            for(j = 0 ; j < index ; ++j){
                if(node[j].name == a){
                    break;
                }
            }
            if(j == index){
                res.push_back(-1.0);
                continue;
            }

            for(k = 0 ; k < index ; ++k){
                if(node[k].name == b){
                    break;
                }
            }
            if(k == index){
                res.push_back(-1.0);
                continue;
            }

            if(a == b){
                res.push_back(1.0);
                continue;
            }

            fill(v,v+index,false);
            v[j] = true;
            res.push_back(dfs(j,k,j));
        }

        return res;
    }
};

2023.5.20

二叉搜索子树的最大键值和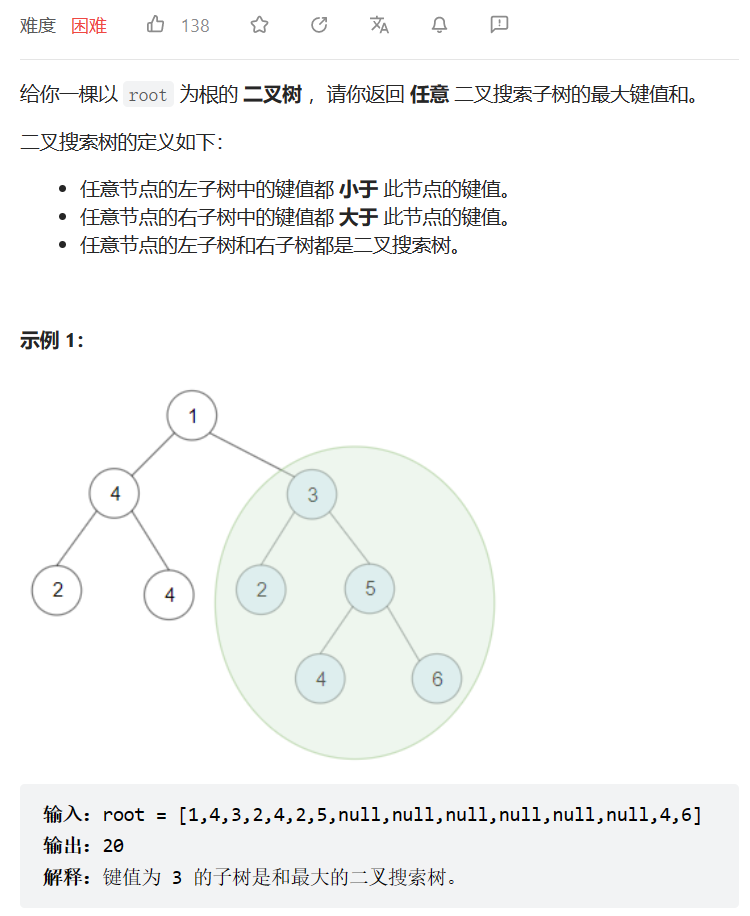

数据范围：

我的思路：

数据量很小，于是递归就可以做了。对于每个节点，我想要判断他是不是二叉搜索树，关键在于：

• 左子树和右子树是二叉搜索树；
• 左子树的最大值小于根节点；
• 右子树的最小值大于根节点；

因此，我利用递归进行计算，当满足上述四个条件时，计算最大键值，和临时结果进行比较。这里最需要注意的是节点状态的存储以及当前节点对应最大键值和的处理。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int max_value = -1000000009;
    unordered_map<TreeNode* , int> ss;
    int getright(TreeNode* root){
        if(root == NULL){
            return -40001;
        }
        while(root->right){
            root = root->right;
        }
        return root->val;
    }
    int getleft(TreeNode* root){
        if(root == NULL){
            return 40000;
        }
        while(root->left){
            root = root->left;
        }
        return root->val;
    }
    int getvalue(TreeNode* root){
        if(root==NULL){
            return 0;
        }
        if(root->left == NULL && root->right == NULL){
            return ss[root] = root->val;
        }
        if(ss.find(root)!=ss.end()){
            return ss[root];
        }
        return ss[root] = getvalue(root->left)+getvalue(root->right)+root->val;
    }
    bool isTrue(TreeNode* root){
        if(root==NULL){
            return true;
        }
        if(root->left == NULL && root->right == NULL){
            max_value = max(max_value,root->val);
            return true;
        }
        bool f1 = isTrue(root->right);
        bool f2 = isTrue(root->left);
        if(f1 && f2 && root->val < getleft(root->right) && root->val > getright(root->left)){
            max_value = max(max_value , getvalue(root));
            return true;
        }
        return false;
    }
    int maxSumBST(TreeNode* root) {
        isTrue(root);
        return max(0,max_value);
    }
};

2023.5.21

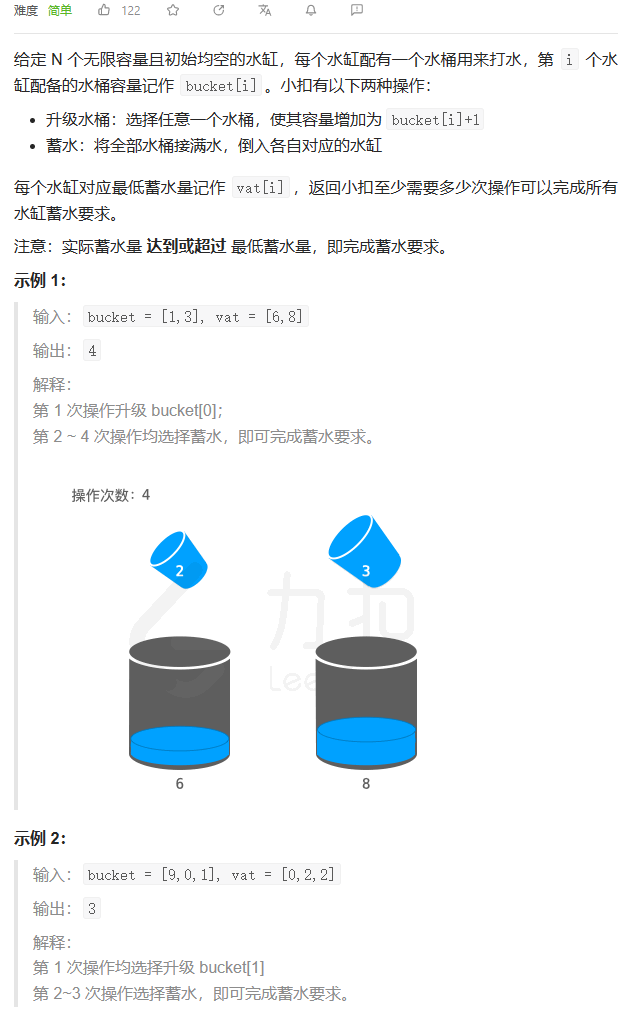
蓄水

数据范围：

我的思路：

首先构建数组存储每个桶当前情况下需要进行多少次操作，然后取最大的操作作为操作数，升级数初始状态下为0。然后对最大操作数的所有点进行升级，比较全部升级之后的结果，如果出现了上升的趋势，则退出循环，返回最小的结果。这里类似于贪心。

class Solution {
public:
    int storeWater(vector<int>& bucket, vector<int>& vat) {
        int n = bucket.size();
        vector<int> res(n);
        int steps = 0;
        int max_value = 0;

        for(int i = 0 ; i < n ; ++i){
            if(vat[i] == 0){
                res[i] = 0;
                continue;
            }
            else if(bucket[i] == 0){
                steps++;
                res[i] = vat[i];
                bucket[i] = 1;
            }
            else{
                res[i] = vat[i]/bucket[i];
                int flag = vat[i]%bucket[i];
                if(flag){
                    res[i]++;
                }
            }
            max_value = max(max_value , res[i]);
        }
        
        int ans = max_value + steps;
        // for(int i = 0 ; i < n ; i++){
        //     cout<<res[i]<<" ";
        // }
        // cout<<endl;

        bool flag = true;
        while(flag){
            int value = 0;
            for(int i = 0 ; i < n ; ++i){
                if(res[i] == max_value){
                    bucket[i]++;
                    res[i] = vat[i]/bucket[i];
                    int f = vat[i]%bucket[i];
                    if(f){
                        res[i]++;
                    }
                    steps++;
                }
                value = max(value , res[i]);
            }
            max_value = value;
            // for(int i = 0 ; i < n ; ++i){
            //     cout<<res[i]<<" ";
            // }
            // cout << steps<<endl;
            if(ans < value + steps){
                break;
            }
            ans = min(ans,value + steps);
        }
        return ans;
    }
};

2023.5.21

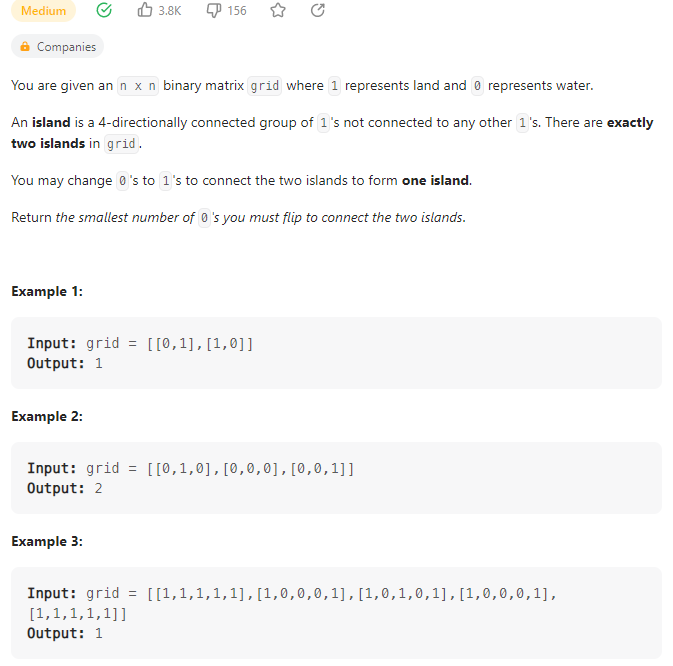
Shortest Bridge

数据范围：

我的思路：

首先需要注意的是只有两个岛屿，因此计算就比较简单了，对某一个岛屿进行特殊标记之后进行bfs遍历，对边界进行拓展，直到边界发生了重叠，停止操作。此时bfs的层数即为所求解；

class Solution {
public:
    int shortestBridge(vector<vector<int>>& grid) {
        int n =grid.size();
        int dx[4] = {0,0,1,-1};
        int dy[4] = {1,-1,0,0};
        queue<pair<int,int>> res;
        bool flag = false;

        //对不同岛屿进行标记
        for(int i = 0 ; i < n ; ++i){
            for(int j = 0 ; j < n ; ++j){
                if(grid[i][j] == 1){
                    grid[i][j] = 2;
                    pair<int,int> p(i,j);
                    queue<pair<int,int>> q;
                    q.push(p);
                    while(!q.empty()){
                        pair<int,int> temp = q.front();
                        q.pop();
                        res.push(temp);
                        for(int k = 0 ; k < 4 ; k++){
                            int xx = dx[k] + temp.first;
                            int yy = dy[k] + temp.second;
                            if(min(xx,yy) >= 0 && max(xx,yy) < n){
                                if(grid[xx][yy] == 1){
                                    grid[xx][yy] = 2;
                                    q.push(make_pair(xx,yy));
                                }
                            }
                        }
                    }
                    flag = true;
                    break;
                }
            }
            if(flag){
                break;
            }
        }

        //从岛屿2开始进行bfs，直到和岛屿1接触；
        int count = 0;
        while(!res.empty()){
            int size = res.size();
            while(size--){
                pair<int,int> temp = res.front();
                res.pop();
                for(int k = 0 ; k < 4 ; ++k){
                    int xx = temp.first + dx[k];
                    int yy = temp.second + dy[k];
                    if(min(xx,yy) >= 0 && max(xx,yy) < n){
                        if(grid[xx][yy] == 0){
                            grid[xx][yy] = 2;
                            res.push(make_pair(xx,yy));
                        }
                        else if(grid[xx][yy] == 1){
                            return count;
                        }
                    }
                }
            }
            count++;
        }

        return count;
    }
};

2023.5.22

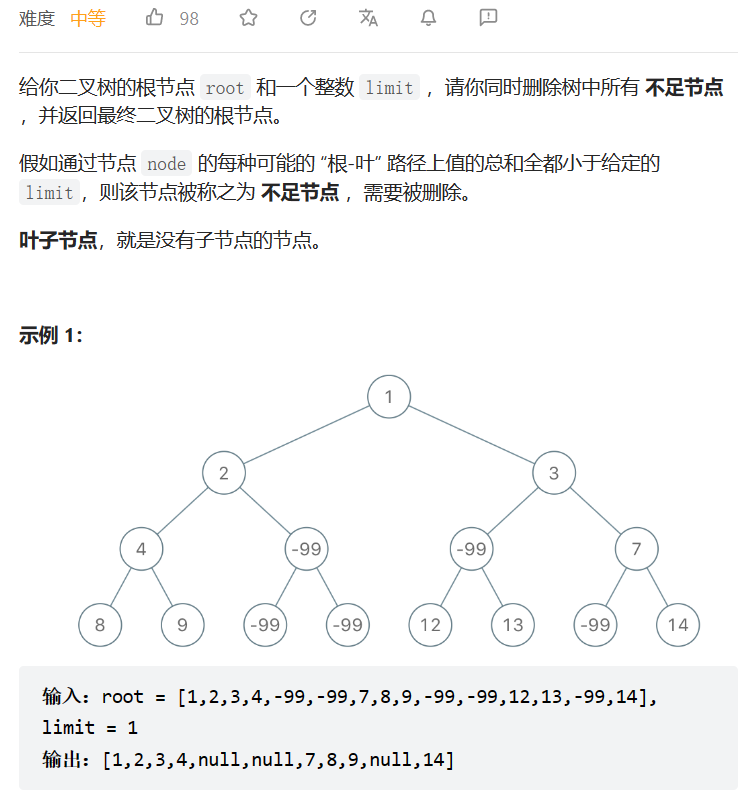
根到叶路径上的不足节点

数据范围：

我的思路：

首先，从顶向下构建一个哈希表，存储前缀和；然后从下到上构建哈希表，存储后缀和；最后对整棵树进行后序遍历，确定是否删除该节点。这里使用的方法较为麻烦，我认为应该有更为简便的方法。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode* , int> mp;
    unordered_map<TreeNode* , int> tmp;
    void get_tmp(TreeNode* root){
        if(root == NULL){
            return;
        }
        if(root->left == NULL && root->right == NULL){
            return;
        }
        else if(root->left == NULL){
            tmp[root->right] = tmp[root] + root->right->val;
        }
        else if(root->right == NULL){
            tmp[root->left] = tmp[root] + root->left->val;
        }
        else{
            tmp[root->left] = tmp[root] + root->left->val;
            tmp[root->right] = tmp[root] + root->right->val;
        }
        get_tmp(root->left);
        get_tmp(root->right);
    }
    int get_max(TreeNode* root){
        if(root == NULL){
            return 0;
        }
        if(root->left == NULL && root->right == NULL){
            return mp[root] = root->val;
        }
        else if(root->left == NULL){
            return mp[root] = get_max(root->right) + root->val;
        }
        else if(root->right == NULL){
            return mp[root] = get_max(root->left) + root->val;
        }
        return mp[root] = max(get_max(root->right) , get_max(root->left)) + root->val;
    }
    TreeNode* isTrue(TreeNode* root, int limit){
        if(root == NULL){
            return root;
        }
        root->left = isTrue(root->left , limit);
        root->right = isTrue(root->right , limit);
        if(mp[root] + tmp[root] - root->val >= limit || mp[root] + tmp[root] - root->val >= limit){
            return root;
        }
        else{
            return NULL;
        }
    }
    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        tmp[root] = root->val;
        get_tmp(root);
        mp[root] = get_max(root);
        root = isTrue(root , limit);
        // for(auto it = mp.begin() ; it!=mp.end() ; it++){
        //     cout<<it->first->val <<" "<< it->second<<endl;
        // }
        return root;
    }
};

2023.5.22

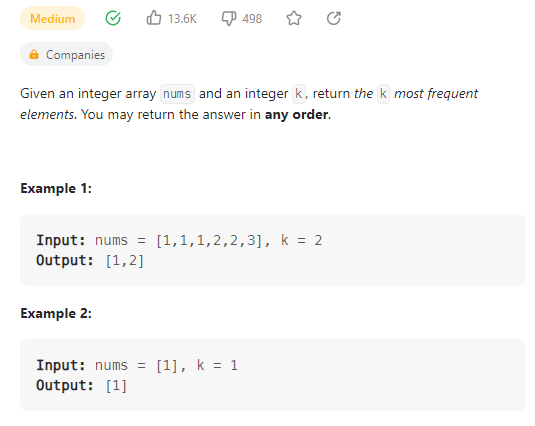
Top K Frequent Elements

数据范围：

我的思路：

第一种方法，构建一个足够大的结构体数组，保存下标和数值，然后对整个数组进行排序，排序过后输出所有下标，这里需要注意的是下标的处理。

struct Node{
    int num;
    int i;
    Node(){
        num = 0;
    }
};

bool cmp(Node a , Node b){
    return a.num > b.num;
}
class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        int n = nums.size();
        const int maxn = 20001;
        Node a[maxn];
        for(int i = 0 ; i < maxn ; ++i){
            a[i].i = i;
        }
        for(int i= 0 ; i < n ; ++i){
            a[nums[i]+10000].num++;
        }
        sort(a,a+maxn,cmp);
        vector<int> res(k);
        for(int i = 0 ; i < k ; ++i){
            res[i] = a[i].i - 10000;
        }
        return res;
    }
};

第二种方法，即优先队列的方法，计数之后将pair传入队列中，保证每次添加之后队列的长度恒定，最后按序输出即可。

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        map<int ,int> mp;
        priority_queue<pair<int , int> , vector<pair<int , int>> , greater<pair<int,int>>> q;
        for(auto num : nums){
            mp[num]++;
        }
        for(auto count : mp){
            q.push({count.second , count.first});
            if(q.size() > k){
                q.pop();
            }
        }
        vector<int> ans;
        while(k--){
            ans.push_back(q.top().second);
            q.pop();
        }
        return ans;
    }
};

2023.5.23

受标签影响的最大值

数据范围：

我的思路：

常规的思路应该是数值和标签同时排序，依据贪心策略每次取最大值，对于取满的标签进行跳过处理，最终得到最优解。但是我的脑子好像比较跳脱，先是构建了一个哈希表，存储标签和优先队列的映射，然后计算numWanted和正常取值的最小值，根据最小值确定最后的结果。

class Solution {
public:
    int largestValsFromLabels(vector<int>& values, vector<int>& labels, int numWanted, int useLimit) {
        unordered_map<int , priority_queue<int , vector<int> , less<int>>> mp;
        int n = values.size();
        for(int i = 0 ; i < n ; i++){
            mp[labels[i]].push(values[i]);
        }
        //cout<<mp[1].top()<<endl;
        
        //计算最小数量；
        int res = 0;
        priority_queue<int , vector<int> , less<int>> q;
        for(auto it = mp.begin() ; it!=mp.end() ; it++){
            int tmp = it->second.size();
            tmp = min(tmp , useLimit);
            // cout<<tmp<<endl;
            res += tmp;
            for(int i = 0 ; i < tmp ; i++){
                q.push(mp[it->first].top());
                mp[it->first].pop();
            }
        }
        int len = min(res,numWanted);
        int ans = 0;
        for(int i = 0 ; i < len ; i++){
            ans += q.top();
            //cout<<ans<<endl;
            q.pop();
        }
        return ans;
    }
};

2023.5.23

Kth Largest Element in a Stream

数据范围：

我的思路：

构建一个长度为k的优先队列，每次返回栈顶元素即可。

class KthLargest {
private:
    int k;
    priority_queue<int, vector<int>, greater<int>> pq;
public:
    KthLargest(int k, vector<int>& nums) {
        this->k = k;
        auto endPointer = nums.begin() + min(k, (int)nums.size());
        pq = priority_queue<int, vector<int>, greater<int>> (nums.begin(), endPointer);
        for(int i = k; i < nums.size(); ++i) {
            pq.push(nums[i]);
            pq.pop();
        }
    }
    
    int add(int val) {
        pq.push(val);
        if(pq.size() > k) pq.pop();
        return pq.top();
    }
};

2023.5.24

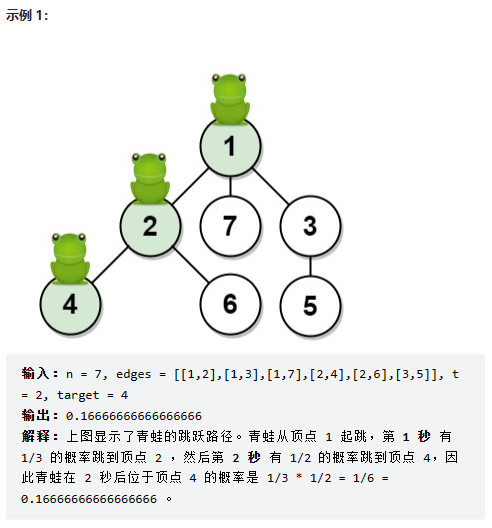
T 秒后青蛙的位置

数据范围：

我的思路：

利用bfs对各点进行遍历，根据时间的变化和目标点是否找到进行break操作。需要注意的是：

• 树的构建，这里我构建了n个集合存储相邻结点，构建状态数组存储是否访问，构建哈希表存储各个节点的到达概率；

class Solution {
public:
    double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
        if(n == 1){
            return 1.0;
        }
        vector<unordered_set<int>> grid(n+1);
        vector<bool> v(n+1,false);
        unordered_map<int , double> mp;
        int m = edges.size();
        int T = 0;
        int res_index = 0;
        int tmp_size = 1;

        for(int i = 0 ; i <= n ; ++i){
            unordered_set<int> temp;
            temp.insert(i);
            grid[i] = temp;
        }
        for(int i = 0 ; i < m ; ++i){
            grid[edges[i][0]].insert(edges[i][1]);
            grid[edges[i][1]].insert(edges[i][0]);
        }
        queue<int> q;
        q.push(1);
        mp[1] = 1;
        v[1] = true;
        bool flag = false;
        while(!q.empty()){
            int nn = q.size();
            while(nn--){
                int temp = q.front();
                q.pop();
                if(temp == target){
                    if(T != t && (grid[temp].size() != 2 || temp == 1)){
                        return 0.0;
                    }
                    flag = true;
                    res_index = temp;
                    break;
                }
                if(grid[temp].size() == 1){
                    continue;
                }
                double tmp = 1.0/(grid[temp].size()-tmp_size);
                if(tmp_size == 1){
                    tmp_size++;
                }
                double index = mp[temp];
                for(auto it = grid[temp].begin() ; it!=grid[temp].end() ; it++){
                    mp[*it] = tmp*index;
                    if(*it!=temp && !v[*it]){
                        v[*it] = true;
                        q.push(*it);
                    }
                }
            }
            if(flag){
                break;
            }
            if(T == t){
                return 0.0;
            }
            T++;
        }
        return mp[res_index];
    }
};

2023.5.24

Maximum Subsequence Score

数据范围：

我的思路：

首先构建pair数组，存储num1和num2，然后根据num2进行排序。构建有限序列，存入num1，当队列数量达到k时，对结果进行计算。

class Solution {
public:
    long maxScore(vector<int>& nums1, vector<int>& nums2, int k) {
        int n = nums1.size();
        vector<vector<int>> pairs(n, vector<int>(2));
        for (int i = 0; i < n; i++) {
            pairs[i][0] = nums2[i];
            pairs[i][1] = nums1[i];
        }
        sort(pairs.begin(), pairs.end(), [](const vector<int>& a, const vector<int>& b) {
            return b[0] < a[0];
        });
        priority_queue<int, vector<int>, greater<int>> pq;
        long res = 0, totalSum = 0;
        for (const vector<int>& pair : pairs) {
            pq.push(pair[1]);
            totalSum += pair[1];
            if (pq.size() > k) {
                totalSum -= pq.top();
                pq.pop();
            }
            if (pq.size() == k) {
                res = max(res, totalSum * pair[0]);
            }
        }
        return res;
    }
};

2023.5.25

差值数组不同的字符串

数据范围：

我的思路：

构建vector比较函数，然后依次遍历即可。

class Solution {
public:
    bool isequal(vector<int> a , vector<int> b){
        int n = a.size();
        for(int i = 0 ; i < n ; ++i){
            if(a[i]!=b[i]){
                return false;
            }
        }
        return true;
    }
    string oddString(vector<string>& words) {
        int n = words.size();
        int len = words[0].length();
        vector<vector<int>> res;
        vector<string> res1;
        bool flag = true;

        for(auto word : words){
            vector<int> tmp;
            for(int j = 1 ; j < len ; ++j){
                int temp = word[j] - word[j-1];
                tmp.push_back(temp);
            }          
            if(res.size() < 2){
                res.push_back(tmp);
                res1.push_back(word);
                if(res.size() == 2){
                    if(isequal(res[0],res[1])){
                        flag = true;
                    }
                    else{
                        flag = false;
                    }
                }
            }
            else{
                if(flag && !isequal(tmp,res[0])){
                    return word;
                }
                else if(!flag && isequal(tmp,res[0])){
                    return res1[1];
                }
                else if(!flag && isequal(tmp,res[1])){
                    return res1[0];
                }
            }
            
        }
        return "";
    }
};

2023.5.25

New 21 Game

数据范围：

我的思路：

class Solution {
public:
    double new21Game(int n, int k, int maxPts) {
        if(k == 0 || n >= k+maxPts){
            return 1.0;
        }
        vector<double> dp(n+1);
        dp[0] = 1.0;
        double w_sum = 1.0;
        double res = 0.0;
        for(int i = 1 ; i <= n ; ++i){
            dp[i] = w_sum/maxPts;
            if(i < k){
                w_sum += dp[i];
            }
            else{
                res += dp[i];
            }
            if(i - maxPts >= 0){
                w_sum -= dp[i-maxPts];
            }
        }
        return res;
    }
};

2023.5.26

Stone Game II

数据范围：

我的思路：

有一点点博弈论的味道，难点在于每次决策如何获得最优解。这里采用的事动态规划的解法，即利用dp[i][j]存储从i开始，当前M值为j的时候Alice的最大石头数量。这里的每一次决策都要取决于下一步对方的收益如何获得最小值。ALICE的决策基础是选择一个最优的x来最小化后缀数组，公式如下：

$$dp[i][j] = max(sufsum[i] - dp[i + X][max(j, X)]) where 1<= X <= 2j;$$

代码如下：

class Solution {
public:
    int stoneGameII(vector<int>& piles) {
        int n = piles.size();
        vector<vector<int>> dp(n+1 , vector<int>(n+1 , 0));
        vector<int> sufsum(n+1 , 0);
        for(int i = n-1 ; i >= 0 ; --i){
            sufsum[i] = sufsum[i+1] + piles[i];
        }
        for(int i = 0 ; i <= n ; ++i){
            dp[i][n] = sufsum[i];
        }
        for(int i = n-1 ; i >= 0 ; i--){
            for(int j = n-1 ; j >= 1 ; j--){
                for(int x=1 ; x <= 2*j && i + x <= n ; x++){
                    dp[i][j] = max(dp[i][j] , sufsum[i] - dp[i+x][max(j,x)]);
                }
            }
        }
        return dp[0][1];
    }
};

2023.5.26

二进制矩阵中的最短路径

数据范围：

我的思路：

喜欢深搜暴力是吧，喜欢回溯是吧？最后还是不如bfs，令人感慨；

int dx[8] = {0,0,1,-1,1,1,-1,-1};
int dy[8] = {1,-1,0,0,-1,1,-1,1};

class Solution {
public:
    // int ans;
    // void dfs(int x , int y , vector<vector<bool>>& v , vector<vector<int>>& grid , int n , int steps){
    //     if(x == n-1 && y == n-1){
    //         if(ans == -1){
    //             ans = steps;
    //         }
    //         else{
    //          ans = min(ans , steps);
    //         }
    //     }
    //     for(int i = 0 ; i < 8 ; ++i){
    //         int xx = x + dx[i];
    //         int yy = y + dy[i];
    //         if(min(xx,yy) >= 0 && max(xx,yy) < n && !v[xx][yy] && grid[xx][yy] == 0){
    //             v[xx][yy] = true;
    //             dfs(xx,yy,v,grid,n,steps+1);
    //             v[xx][yy] = false;
    //         }
    //     }
    // } 
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        if(grid[0][0] != 0 || grid[n-1][n-1] != 0){
            return -1;
        }
        vector<vector<bool>> v(n,vector<bool>(n,false));
        queue<pair<int , int>> q;
        int steps = 0;
        bool flag = false;

        q.push(make_pair(0,0));
        v[0][0] = true;
        while(!q.empty()){
            int nn = q.size();
            while(nn--){
                pair<int , int> p = q.front();
                q.pop();             
                if(p.first == n-1 && p.second == n-1){
                    flag = true;
                    break;
                }
                for(int i = 0 ; i < 8 ; ++i){
                    int xx = p.first + dx[i];
                    int yy = p.second + dy[i];
                    if(min(xx,yy)>=0 && max(xx,yy) < n && !v[xx][yy] && grid[xx][yy] == 0){
                        v[xx][yy] = true;
                        q.push(make_pair(xx,yy));
                    }
                }
            }
            steps++;
            if(flag){
                return steps;
            }
        }
        return -1;
    }
};

2023.5.27

Stone Game III

数据范围：

我的思路：

这道题和之前那一道题比较类似，唯一的不同点是每次取值的范围变小了，即只能取1、2、3个石头堆，因此这里还是使用动态规划的方法，从最后的情况往前倒推。先来看一看公式：

$$dp[i]=max(dp[i],take - (i+k+1 < n? dp[i+k+1]:0)$$

dp[i]代表Alice忽略前0-i项石头堆，只考虑i+1-n的最大得分。这里很符合我们的逻辑，有一点点贪心的算法，每次都获得最优，从而获得全局的最优。之后就是对dp[i]的计算了，这里的take代表i-i+k这几个堆的石头总数，也就是这一步Alice得到的分数，这个分数和dp[i+k+1]进行比较即可。

根据我们之前的推导，dp[i+k+1]代表Alice忽略前0-i+k+1个石头堆得到的最高分，其实这里也是代表了Bob忽略前0-i+k+1个石头堆得到的最低分。从而推导式分析完成。

class Solution {
public:
    string stoneGameIII(vector<int>& stoneValue) {
        int n = stoneValue.size();
        vector<int> dp(n,-1e9);
        for(int i = n-1 ; i >= 0 ; --i){
            for(int k = 0 ,take = 0; k < 3 && i+k < n ; ++k){
                take += stoneValue[i+k];
                dp[i] = max(dp[i],take - (i+k+1 < n ? dp[i+k+1] : 0));
            }
        }
        if(dp[0] > 0){
            return "Alice";
        }
        if(dp[0] < 0){
            return "Bob";
        }
        return "Tie";
    }
};

2023.5.27

大样本统计

数据范围：

我的思路：

这里最不好求的就是中位数，中位数我是维护了一个哈希表，当遍历数量超过半数时计算中位数。感觉双指针可能会好一些吧，毕竟logn是吧。

class Solution {
public:
    vector<double> sampleStats(vector<int>& count) {
        int n = count.size();
        double size = 0.0;
        map<int , int> mp;

        double max_value;
        double min_value;
        double last_value = -1;
        double last_count = 0;
        double mean = 0;
        double median;
        int mode_count = 0;
        double mode;
        
        int i = 0;
        bool flag = true;
        
        while(i < n){
            while(i < n && count[i] == 0){
                i++;
            }
            if(flag){
                min_value = i;
                flag = false;
            }
            if(i < n){
                size += count[i];
                mp[i] = count[i];
                if(count[i] > mode_count){
                    mode_count = count[i];
                    mode = i;
                }
                last_value = i;
                i++;
            }
        }
        max_value = last_value;
        last_value = mp.begin()->first;
        mean /= size;

        int half = size/2 + 1;
        bool f = true;
        for(auto it = mp.begin() ; it!=mp.end() ; it++){
            if(f && last_count + it->second >= half){
                if(int(size)%2 == 0){
                    if(half - last_count == 1){
                        median = (it->first + last_value)/2.0;
                    }
                    else{
                        median = it->first;
                    }
                }
                else{
                    median = it->first;
                }
                f = false;
            }
            mean += (it->second/size * it->first);
            last_value = it->first;
            last_count += it->second;
        }
        return {min_value , max_value , mean , median , mode};
    }
};

2023.5.30

Design HashSet

数据范围：

我的思路：

直接构建长度不定的数组然后每次进行ON的遍历了，感觉能优化的地方有很多，比如res的erase操作等等。

class MyHashSet {
public:
    vector<int> res;
    int size = 0;
    MyHashSet() {
        size = 0;
    }
    
    void add(int key) {
        int i;
        for(i = 0 ; i < size ; ++i){
            if(res[i] == key){
                break;
            }
        }
        if(i == size){
            res.push_back(key);
            size++;
        }
    }
    
    void remove(int key) {
        int i;
        for(i = 0 ; i < size ; ++i){
            if(res[i] == key){
                break;
            }
        }
        if(i != size){
            size--;
            res.erase(res.begin()+i);
        }
    }
    
    bool contains(int key) {
        int i;
        for(i = 0 ; i < size ; ++i){
            if(res[i] == key){
                return true;
            }
        }
        return false;
    }
};

/**
 * Your MyHashSet object will be instantiated and called as such:
 * MyHashSet* obj = new MyHashSet();
 * obj->add(key);
 * obj->remove(key);
 * bool param_3 = obj->contains(key);
 */

2023.5.30

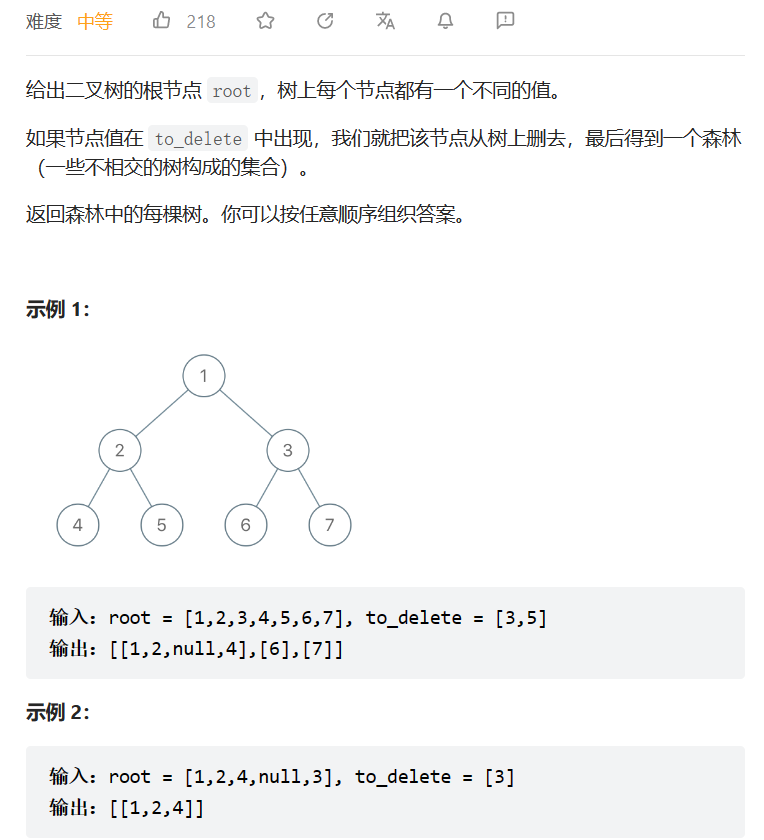
删点成林

数据范围：

我的思路：

首先层次遍历找出所有的被删除点，然后将父节点和删除节点的连接取消，最后将所有删除节点存在的孩子节点压入结果数组中。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        int n = to_delete.size();
        queue<TreeNode*> q;
        unordered_set<int> ss;
        vector<TreeNode*> tmp;
        vector<TreeNode*> ans;

        for(auto td : to_delete){
            ss.insert(td);
        }
        q.push(root);
        if(ss.find(root->val) != ss.end()){
            tmp.push_back(root);
        }
        else{
            ans.push_back(root);
        }
        while(!q.empty()){
            int nn = q.size();
            while(nn--){
                TreeNode* temp = q.front();
                q.pop();
                TreeNode* l = temp->left;
                TreeNode* r = temp->right;
                if(l){
                    if(ss.find(l->val) != ss.end()){
                        temp->left = NULL;
                        tmp.push_back(l);
                    }
                    q.push(l);
                }
                if(r){
                    if(ss.find(r->val) != ss.end()){
                        temp->right = NULL;
                        tmp.push_back(r);
                    }
                    q.push(r);
                }
            }
        }
        
        int len = tmp.size();
        for(int i = 0 ; i < len ; ++i){
            if(tmp[i]->left){
                ans.push_back(tmp[i]->left);
            }
            if(tmp[i]->right){
                ans.push_back(tmp[i]->right);
            }
        }

        return ans;
    }
};

2023.5.31

Design Underground System

数据范围：

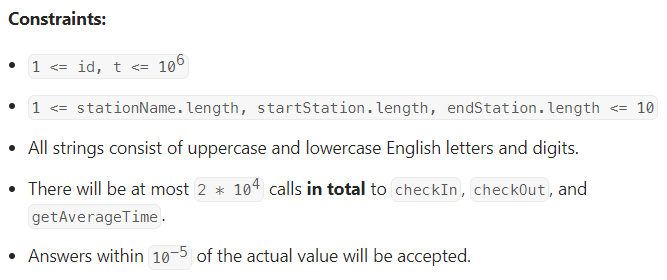
我的思路：

喜欢我哈希表恩造吗，只能说可惜数据量太少，由于map不支持pair类型的键值，因此直接将出发地和到达地进行字符串合并，中间添加间隔符（为了跳过重复的字段）。

class UndergroundSystem {
public:
    unordered_map<int , pair<string , int>> begin_mp;
    unordered_map<string , double> avg;
    unordered_map<string , int> size_mp;
    
    UndergroundSystem() {
        
    }
    
    void checkIn(int id, string stationName, int t) {
        begin_mp[id] = make_pair(stationName , t);
    }
    
    void checkOut(int id, string stationName, int t) {
        string begin_s = begin_mp[id].first;
        int begin_t = begin_mp[id].second;
        string p = begin_s + "0" + stationName;
        if(avg.find(p) != avg.end()){
            int size = size_mp[p];
            double res = avg[p];
            avg[p] = (res*size + t - begin_t)/(size+1);
            size_mp[p] = size+1;
        }
        else{
            avg[p] = (double)(t-begin_t);
            size_mp[p] = 1;
        }
    }
    
    double getAverageTime(string startStation, string endStation) {
        string tmp = startStation+"0"+endStation;
        return avg[tmp];
    }
};

/**
 * Your UndergroundSystem object will be instantiated and called as such:
 * UndergroundSystem* obj = new UndergroundSystem();
 * obj->checkIn(id,stationName,t);
 * obj->checkOut(id,stationName,t);
 * double param_3 = obj->getAverageTime(startStation,endStation);
 */

2023.5.31

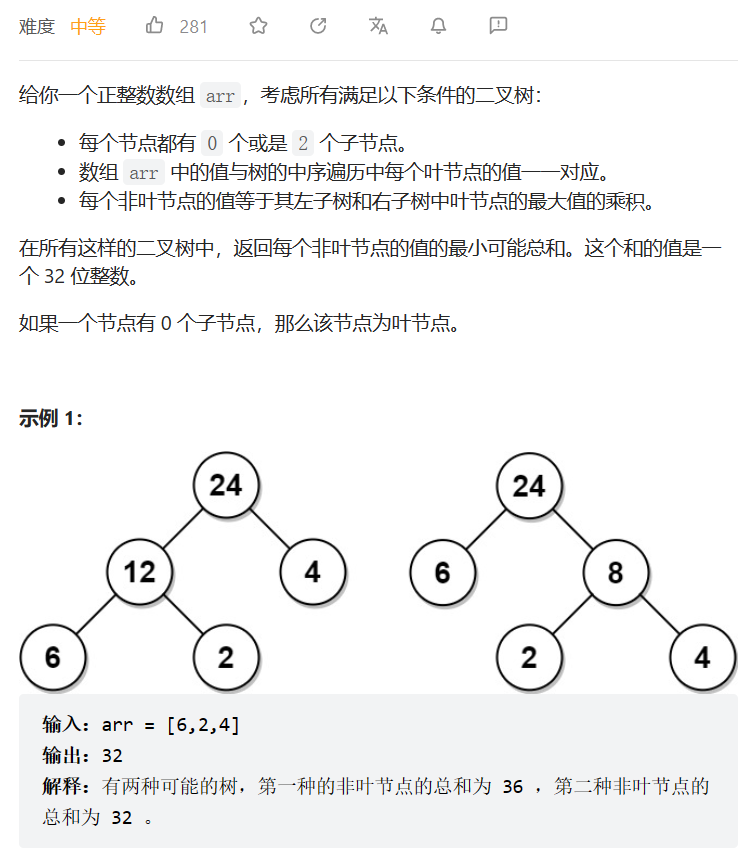
叶值的最小代价生成树

数据范围：

我的思路：

单调栈，从左到右遍历所有的元素，从低向上构建整个二叉树，类似于霍夫曼编码。

class Solution {
public:
    int mctFromLeafValues(vector<int>& arr) {
        int res = 0;
        stack<int> stk;
        for (int x : arr) {
            while (!stk.empty() && stk.top() <= x) {
                int y = stk.top();
                stk.pop();
                if (stk.empty() || stk.top() > x) {
                    res += y * x;
                } else {
                    res += stk.top() * y;
                }
            }
            stk.push(x);
        }
        while (stk.size() >= 2) {
            int x = stk.top();
            stk.pop();
            res += stk.top() * x;
        }
        return res;
    }
};