机器翻译：基础与模型学习笔记——统计机器翻译

[TOC]

基于词的机器翻译建模

传统翻译过程：

• 分析：将源语言句子表示为适合机器翻译的结构，分词；
• 转换：每个单词转换成目标语言单词；
• 生成：将目标语言译文转换成合乎语法的句子；

单词统计机器翻译的基本框架：

• 训练：首先根据双语平行数据获取参数，最终得到将源语言翻译成目标语言的概率所需参数；
• 解码：对测试集中的新句子，搜索尽可能高分的译文结果进行输出；

双语平行数据训练过程中往往是通过统计两个单词在两句中的出现概率获取单词互译概率的，公式如下所示：

$$\begin{array}{rcl}P(x\leftrightarrow y;s,t)&\equiv&P(x,y;s,t)\\&=&\frac{c(x,y;s,t)}{\sum_{x',y'}c(x',y';s,t)}\end{array}$$

其中s代表source ，t代表target ， x和y分别是两句中的单词，c(x,y;s,t)代表xy在st中共同出现的次数，这里可能需要使用平滑对未出现的词进行处理，这个公式只是对单个句对进行处理，可以推广到大规模数据处理中。

句子级翻译模型的基本结构：

• 想要求解P(T|S)，需要构建一个函数，即g（s,t），使得翻译结果t出现的可能性越大，g的值越大。
• 构建g往往需要利用词对齐构成词对，然后将构成词对的概率进行排列组合，相乘得到最高评分的即为最佳译文，可见词对齐对译文的质量影响很大。
• 最后利用n-gram模型进行译文流畅度的惩罚，保证语序的正确。
• j解码：搜索最优解。（小数据统计，大数据贪心）

$$P(t|s)\quad\equiv\quad\frac{g(s,t)}{\sum_{t'}g(s,t')}$$

\begin{array}{rcl}g(s,t)&=&\prod_{(j,i)\in\widehat{A}}P(s_j,t_i)\end{array}\

惩罚项计算：

$$\begin{array}{rcl}P_{\mathrm{lm}}(t)&=&P_{\mathrm{lm}}(t_1...t_l)\\&=&P(t_1)\times P(t_2|t_1)\times P(t_3|t_2)\times...\times P(t_l|t_{l-1})\end{array}$$

噪声信道模型

定义：目标语言t被看做是由源语言s通过一个有噪音的信道获得的，只需要知道s和信道的性质，这里着重介绍IBM模型的基本构成。

$$\begin{array}{rcl}\widehat{t}&=&\mathop{\mathrm{argmax}}_tP(t|s)\\&=&\mathop{\mathrm{argmax}}_t\frac{P(s|t)P(t)}{P(s)}\\&=&\mathop{\mathrm{arg\max}}_tP(s|t)P(t)\end{array}$$

其中P(s|t)代表反向的翻译模型，考量的是翻译质量；同时P（t）的参加保证了模型内的译文流畅度。

因此该模型的构建过程如下所示：

• 建模：构建P(s|t)和P(t)的数学模型；
• 训练：获得最优的超参数；
• 解码：最优化过程；

非对称词对齐方法

定义：对源语言进行约束，每个单词进行目标语言的对应，同时引入空对齐的思想，在保证译文质量的情况下提高流畅程度。

翻译模型的应用：将所有词对齐的实现概率作为s翻译成t的概率计算公式，具体的过程如下所示：

$$\begin{matrix}P(s|t)&=&\sum_aP(s,a|t)\end{matrix}$$

这里就到了IBM模型的关键之处，即计算各种词对组合的概率：

• 取源语言固定长度m作为研究对象，进行分词操作得到sj，此时sj不存在顺序关系；
• 找到对齐关系，即根据译文t、源文长度m、已经生成的s(j-1)和a(j-1)，得到a(j)对齐关系，这里利用的是源语言中的句中关系；
• 结合上述的对齐关系，生成第j个位置的源语言单词sj；

$$P(s,a|t)\quad=\quad P(m|t)\prod_{j=1}^{m}P(a_j|a_1^{j-1},s_1^{j-1},m,t)P(s_j|a_1^{j},s_1^{j-1},m,t)$$

IBM模型构建

上述的两种方法都在IBM模型中有所体现，但是依旧存在部分问题，即对齐词对的数量是呈现指数增长的，不可能通过枚举实现。此外，每一步需要的参数较多，计算效率低，需要对参数进行压缩。

压缩的过程就是对三个表达式进行精简：

• 假设源语言句子长度生成概率服从均匀分布；
• 假设对齐概率只依赖于译文的位置，呈现均匀分布；
• 源语言单词的生成只和形成词对的元素有关；

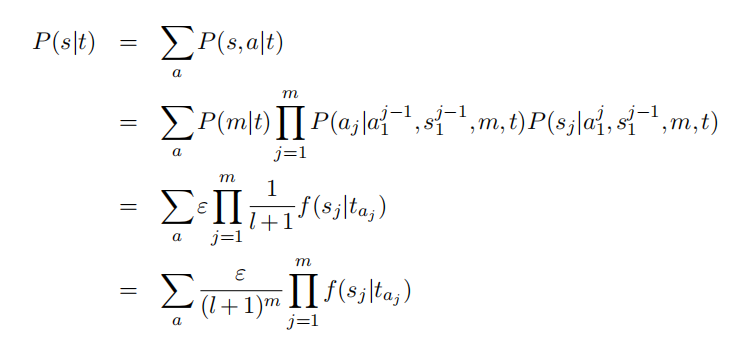
最后化简得到IBM模型1的最终表达式：

$$\text{IBM 模型 1:}\quad P(s|t)\quad=\quad\frac{\varepsilon}{(l+1)^m}\prod_{j=1}^m\sum_{i=0}^lf(s_j|t_i)$$

基于扭曲度和繁衍率的模型

提出背景：机器翻译存在的两个挑战，即调序问题和一对多翻译问题（一个词往往会被翻译成多个词，二者的含义相同），因此扭曲度和繁衍率的提出就是对上述IBM模型1的提升。

**扭曲度：**这个指标和调序距离相关，调序距离越大，扭曲度也越大。那么，什么是调序呢？调序代表相较于顺序翻译产生位置偏移，在完成各个单词翻译之后进行顺序调整，这里就会出现位移，也就是扭曲度。下面的对齐矩阵阐述了调序的结果：

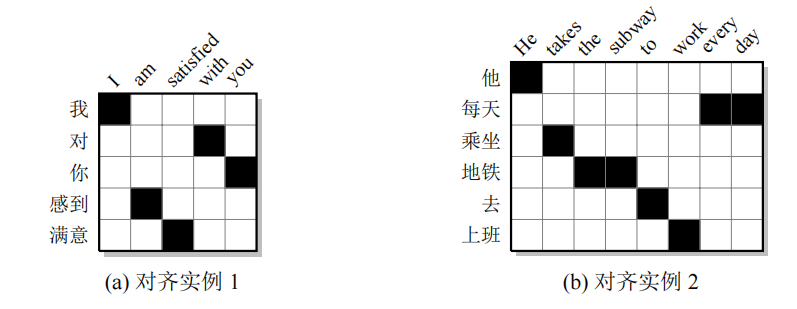
应用扭曲度的思想推翻了之前IBM模型1对于词对齐关系为均匀分布的假设，这里认为词对齐是有一定的倾向性的，它和源语言单词的位置和目标语言单词的位置有关，公式如下：

$$P(a_j|a_1^{j-1},s_1^{j-1},m,t)\quad\equiv\quad a(a_j|j,m,l)$$

可以看到，基于前一组对齐关系、前一个位置的源语言、源语言长度和译文对当前对齐关系进行分析，可以转化成对位置j的对齐关系研究。只对IBM模型1三大假设中对齐关系呈现均匀分布进行更改，得到IBM模型2的数学表述：

$$P(s|t)\quad=\quad\varepsilon\prod_{j=1}^m\sum_{i=0}^la(i|j,m,l)f(s_j|t_i)$$

HMM模型（Hidden Markov Model）：综合IBM的两种模型，HMM认为单词和单词之间存在一定的联系，对齐的概率不应该关注于单词本身的位置j，而是关注对齐位置之间的差距：

$$P(a_j|a_1^{j-1},s_1^{j-1},m,t)\quad\equiv\quad P(a_j|a_{j-1},l)$$

这里的aj-aj-1之间的关系可以通过隐马尔科夫模型进行计算，最终得到的数学表述为：

$$P(s|t)~=~\sum_aP(m|t)\prod_{j=1}^mP(a_j|a_{j-1},l)f(s_j|t_{a_j})$$

基于繁衍率的模型

繁衍率的引入：上述的模型都是对单词的相对位置以及对齐关系的相对位置进行研究，而一对多的问题没有完全解决，不能够对短语-单词的翻译类型进行很好的对齐，具体过程如下所示：

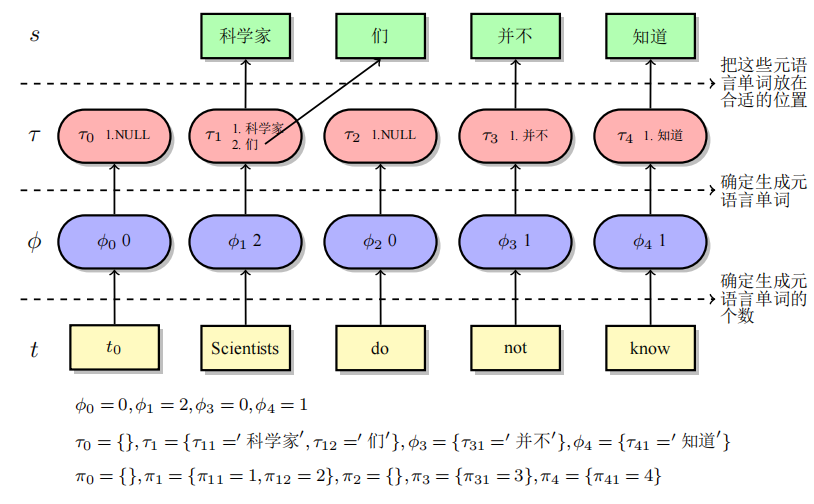
上图阐述了如何应用产出率从英文转换成中文的过程。τ 和 π分别代表生成的源语言单词、单词在源语言中的位置。这里的π就是我们上文提到的扭曲度。因此源语言句子和译文的对应关系可以通过所有源语言单词和居中位置表示如下：

$$P(s,a|t)\quad=\quad\sum_{<\tau,\pi>\in<s,a>}P(\tau,\pi|t)$$

$$\begin{aligned} P(\tau,\pi|t)& =\prod_{i=1}^lP(\varphi_i|\varphi_1^{i-1},t) \times P(\varphi_0|\varphi_1^l,t)\times \\ &\prod_{i=0}^l\prod_{k=1}^{\varphi_i}P(\tau_{ik}|\tau_{i1}^{k-1},\tau_{1}^{i-1},\varphi_{0}^{l},t)\times \\ &\prod_{i=1}^l\prod_{k=1}^{\varphi_i}P(\pi_{ik}|\pi_{i1}^{k-1},\pi_{1}^{i-1},\tau_{0}^l,\varphi_{0}^l,t)\times \\ &\prod_{k=1}^{\varphi_0}P(\pi_{0k}|\pi_{01}^{k-1},\pi_1^l,\tau_0^l,\varphi_0^l,t) \end{aligned}$$

P(τ,π*|*t)之所以用这种形式，主要是对内部实现进行拆分，更容易理解：

• 第一行代表两部分内容，一是对应繁衍度的生成概率，主要影响因素为前一个区间产出率和译文；二是空标记的生成概率，依赖于整体产出率以及译文；
• 第二行代表目标单词生成第k个源语言单词的概率，影响因素为前k-1单词、前i-1个已翻译的源语言短语、整体产出率以及译文；
• 第三行代表目标单词生成第k个源语言单词的相对位置概率，影响因素为前k-1个单词相对位置、前i-1个已翻译的源语言短语位置、整体已生成的源语言单词、整体繁衍度以及译文；
• 第四行对i=0进行建模，讨论空标签在源语言中的位置。

对上述涉及的五部分内容进行化简，得到了我们的IBM模型3：

$$\begin{array}{rcl}P(\varphi_i|\varphi_1^{i-1},t)&=&P(\varphi_i|t_i)\\P(\tau_{ik}=s_j|\tau_{i1}^{k-1},\tau_1^{i-1},\varphi_0^t,t)&=&t(s_j|t_i)\\P(\pi_{ik}=j|\pi_{i1}^{k-1},\pi_1^{i-1},\tau_0^l,\varphi_0^l,t)&=&d(j|i,m,l)\end{array}$$

$$\prod\limits_{k=1}^{\varphi_0}P(\pi_{0k}|\pi_{01}^{k-1},\pi_{1}^{l},\tau_{0}^{l},\varphi_{0}^{l},t)\quad=\quad\frac{1}{\varphi_{0}!}$$

$$P(s|t)\quad=\quad\sum\limits_{a_1=0}^{l}\cdots\sum\limits_{a_m=0}^{l}\Big[\bigl(\begin{matrix}m-\varphi_0\\\varphi_0\end{matrix}\bigr)p_0^{m-2\varphi_0}p_1^{\varphi_0}\prod\limits_{i=1}^{l}\varphi_i!n(\varphi_i|t_i)\\ \times\prod_{j=1}^mt(s_j|t_{a_j})\times\prod_{j=1,a_j\neq0}^md(j|a_j,m,l)\Big]$$

这里对公式简化过程进行分析。前三个公式只是对参数进行简化，其内部含义并未发生变化。其中d(j*|*i,m,l)被称为扭曲度函数。

然后是空标签的位置生成概率判定，其现实含义就是在每次生成一个源语言单词时都要考虑——是否在所有元素之间穿插空标签？因此得到的结果是阶乘的倒数，最后的公式中将该系数转换成了一个简单的二项分布，便于理解。

**IBM模型3解决了一个源语言单词到多个目标语言单词的问题，但是没有解决多源语言短语到一个目标语言单词的问题。**IBM模型4引出了Brown聚类等方法获取词类信息，从而把目标语言和源语言的单词映射到单词的词类。之后的IBM模型5对不存在的句子进行了约束，但仍旧存在缺陷。下面对本节介绍的IBM模型进行梳理。

模型	特点	缺陷
模型1	提出三大假设，应用非对称词对齐和噪声信道模型	无法解决一对多的问题
模型2	推翻对齐关系呈现均匀分布的假设，同时引入扭曲度和隐马尔科夫模型，对单词位置、词对齐的位置进行深入分析	无法解决一对多的问题
模型3	基于繁衍度继续研究一对多问题，将词对齐方法进一步拓展，考虑词与词之间的关系	无法解决多对一的问题
模型4	聚类方法获取此类信息，使用概念单元进行对齐，同一词类归纳至同一个概念单元中	部分概率被分配到不可能的句子上，导致运算量过大
模型5	在放置一个源语言单词的时候检查当前位置是否已经放置了单词，如果没有放置，将防止过程赋予一定的概率，否则视为不可能事件	存在逻辑缺陷，判断一个句子是否良好的指标质量较差

基于短语的模型

背景：分词进行独立的翻译明显没有考虑词组的本身定义，如将红茶翻译为red tea而不是black tea。因此，更大粒度的翻译单元十分重要。

翻译中的短语信息

有了短语的参与，结合之前的n-gram模型，我们能够很容易得到以下的推演过程：

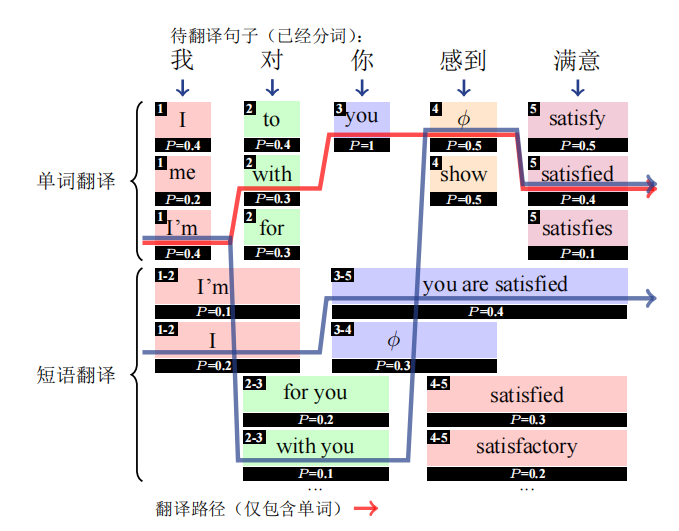
首先是对分词结果进行枚举（单词翻译和短语翻译），然后分析每一条翻译路径的质量。我个人认为只是对对应关系进行了扩充，类比于扩充了数据集，比较好理解。目前，实现短语翻译模型有四个基本的目标：

• 翻译的统计建模问题；如何构建数学公式表述源语言到目标语言的关系；
• 短语翻译获取：分词方法；
• 调序问题：分词结果如何匹配；
• 解码问题：译文质量评价；

区别于单词翻译模型，数据的特征因为词组的加入得到了扩充，涉及的基本特征大致如下：

• 最主要：短语翻译概率（包括组成的单词话翻译概率）；
• 流畅度：n-gram、译文长度；
• 模型复杂度：翻译规则数量、被翻译为空的单词；
• 其他：结合模型特点；

数学建模——针对第一个问题

首当其冲的就是计算P(t|s)的基本公式：

$$P(t|s)\approx\sum_{d\in D_{n-\text{best}}}P(d,t|s)$$

其中d代表一个推导关系，右侧的式子是对不同推导关系进行求和计算翻译精度，这里使用的top-n主要是为了减少计算量。

此外就是利用对数线性模型进行判别，找到势函数mscore达到最大的d：

$$\begin{array}{rcl}\hat d&=&\arg\max_d\frac{\exp(score(d,t,s))}{\sum_{d',t'}\exp(score(d',t',s))}\\&=&\arg\max_d\exp(score(d,t,s))\end{array}$$

整体而言，基于短语的机器翻译系统流程如下所示：

短语抽取——针对第二个问题

短语的抽取依赖于语料的选择以及训练的方法，语料采用平行双语，训练的方法和词对齐类似，是基于双语的矩阵进行的：

确定了抽取方法，如何衡量抽取结果的好坏呢？翻译的好坏往往体现在短语的翻译概率上，可以通过拆分短语获得包含单词的频率，利用上述的IBM模型概率求和得到短语出现概率，最终得到短语表。

翻译调序建模

**基于距离的调序：**扭曲度，一般认为翻译之后的单词顺序不会发生变化，如果发生变化就是调序。这里将调序的相对位移作为特征保存，但是这一方法得到的模型只能适用于特定的两种语言，无法进行广泛的推广。

**基于方向的调序：**判断两个双语短语在源语言端的调序情况，也称为MSD模型。

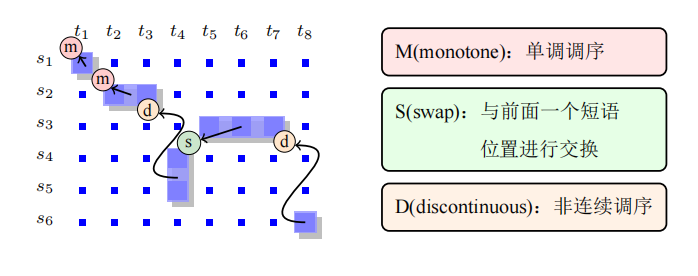
对于整体的调序方法，存在以下的公式计算：

$$P(o|s,t,a)~=~\prod_{i=1}^KP(o_i|\bar{s}_{a_i},\bar{t}_i,a_{i-1},a_i)$$

其中，o代表整体的顺序，oi代表第i个短语的调序方向。需要注意的是，这里的MSD可以不只是和前一个单词的构成的特征，也可以逆序形成特征。

**基于分类的调序：**基于以上的六个特征，完全可以对调序情况进行归类，这里可以使用传统的SVM、最大熵方法，也可以使用最新的神经网络模型进行计算。

基于句法的模型

背景：基于短语的模型往往会存在大范围的短语依赖，长短语跨越较长语段形成的关系往往会使数据系数。如果像编译原理一样对句子构建语法树会使扭曲度较高的短语和目标语言的距离更近。

基于层次短语的模型

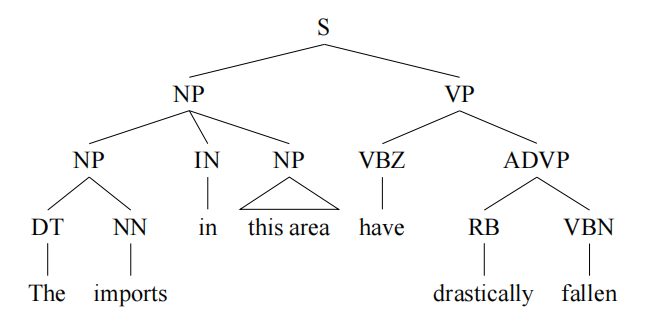
长短语出现的数据稀疏问题，说明长距离的调序需要额外的机制才能更好地处理。层次短语模型就是对语法树各层的描述，如下面的定语从句的翻译过程：

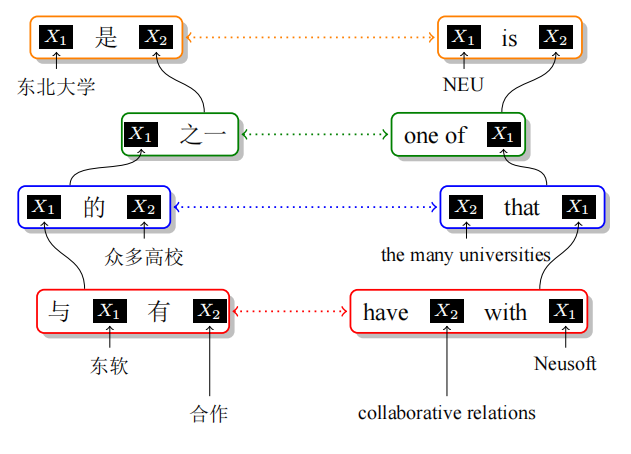
上述过程很像递归过程，将整体看做一个翻译模板，然后根据主谓宾进行划分，内部进行细化的翻译处理，直到最小的翻译单元，这个递归过程是如何用数学表述呢？同步上下文无关文法就显得格外重要了。其简单的数学描述如下所示：

$$\begin{array}{rcl}\mathrm{S}&\to&\langle\mathrm{NP}_1\text{希望}\mathrm{VP}_2,\quad\mathrm{NP}_1\text{wish to VP}_2\rangle\\\mathrm{VP}&\to&\langle\text{对}\mathrm{NP}_1\text{感到}\mathrm{VP}_2,\quad\mathrm{be}\mathrm{VP}_2\text{wish}\mathrm{NP}_1\rangle\\\mathrm{NN}&\to&\langle\text{强大},\quad\mathrm{strong}\rangle\end{array}$$

相关知识

平均互信息

平均互信息与条件熵 - 知乎 (zhihu.com)

$$I(X;Y)=E[I(x,y)]=H(X)-H(X\mid Y)$$

互信息=先验不确定性-后验不确定性 = 不确定性的减少量，常用来表示X和Y 之间的密切程度，呈现正相关的性质，系数越大二者的关系越密切。

Brown聚类方法

Brown Clustering算法和代码学习-CSDN博客

基于n-gram模型和马尔科夫链模型，整体的方法是构建一个词料库，将库内的前C个词分配到不同的C个类中，将词频最高的词添加到一个新的类中，然后将C+1个类进行聚合得到C个类，以此类推，最终得到想要的类数。

算法的实现：主要是依靠n-gram和马尔科夫模型的评价函数构建

$$\begin{array}{rcl}L(\pi)&=&\sum_{w_1w_2}\frac{C(w_1w_2)}{T-1}\log\Pr\left(c_2\mid c_1\right)\Pr\left(w_2\mid c_2\right)\\&=&\sum_{c_1c_2}\frac{C(c_1c_2)}{T-1}\log\frac{\Pr\left(c_2\mid c_1\right)}{\Pr\left(c_2\right)}+\sum_{w_2}\frac{\sum_wC(ww_2)}{T-1}\log\underbrace{\Pr\left(w_2\mid c_2\right)\Pr\left(c_2\right)}_{\mathbf{Pr}(w_2)}.\end{array}$$

$$\begin{aligned} L(\pi)& =\quad\sum_{w}\Pr\left(w\right)\log\Pr\left(w\right)+\sum_{c_{1}c_{2}}\Pr\left(c_{1}c_{2}\right)\log\frac{\Pr\left(c_{2}\mid c_{1}\right)}{\Pr\left(c_{2}\right)} \\ &=\quad-H(w)+I(c_{1},c_{2}), \end{aligned}$$

可以看出，信息熵对于模型的评价是没有帮助的，毕竟每个单词的频率是固定的。因此评价的影响因素为相邻两类的平均互信息。

Viterbi方法

统计机器翻译常用的方法，这里先讲一讲Viterbi方法的基本原理：它是一种动态规划算法，用于寻找最有可能产生观测事件序列的隐含状态序列，常用于马尔科夫模型。

维特比算法(viterbi)原理以及简单实现 - 知乎 (zhihu.com)

同步上下文无关文法

和编译原理中的上下文无关文法不同，因为需要考虑的是源语言和目标语言之间的关系，原始的四元集合不适用，这里是五部分组成（N,Ts,Tt,I,R）

• N：非终结符
• Ts：源语言的终结符；
• Tt：目标语言的终结符；
• I：起始的非终结符；
• R：规则集合；

Future Work

• 根据扭曲度而延伸出来的模型，这种偏差可以用于对调序的建模，我认为可以对扭曲度相关的最新结果进行研读，讨论可能性；
• 基于繁衍度的模型对译文额长度进行预测，如何提高预测的精度等等；