每日一题整理——2023.10

10.12

Find in Mountain Array

给出一个山数组，找出给定元素的最小序号，需要注意的是山数组的形式为get()形式，且使用的次数不能超过100次。

我的思路：看了一下数据范围，10^4，只能二分做，这里先找到最大元素，然后两边分别二分，一共用了三个二分，需要注意边界。

/**
 * // This is the MountainArray's API interface.
 * // You should not implement it, or speculate about its implementation
 * class MountainArray {
 *   public:
 *     int get(int index);
 *     int length();
 * };
 */

class Solution {
public:
    int findInMountainArray(int target, MountainArray &mountainArr) {
        int start = 0;
        int n = mountainArr.length();
        int end = n-1;
        int mid;
        while(start < end){
            mid = start + (end - start)/2;
            if(mountainArr.get(mid) > mountainArr.get(mid+1)){
                end = mid;
            }
            else if(mountainArr.get(mid) < mountainArr.get(mid+1)){
                start = mid+1;
            }
        } 
        int start1 = mid;
        int end1 = n-1;
        end = start;
        start = 0;
        while(start <= end){
            mid = start + (end-start)/2;
            if(mountainArr.get(mid) == target){
                return mid;
            }
            else if(mountainArr.get(mid) > target){
                end = mid-1;
            }
            else{
                start = mid+1;
            }
        }
        while(start1 <= end1){
            mid = start1 + (end1 - start1)/2;
            if(mountainArr.get(mid) == target){
                return mid;
            }
            else if(mountainArr.get(mid) < target){
                end1 = mid-1;
            }
            else{
                start1 = mid+1; 
            }
        }
        return -1;
    }
};

10.13

避免洪水泛滥

数据范围：

我的思路：

大致的思路就是贪心+二分，遍历时记录所有可抽水的日期索引，每次出现洪水时找最近的晴天抽水（二分），最后得到结果。

class Solution {
public:
    vector<int> avoidFlood(vector<int>& rains) {
        vector<int> ans(rains.size() , 1);
        set<int> st;
        unordered_map<int , int> mp;
        for(int i = 0 ; i < rains.size() ; ++i){
            if(rains[i] == 0){
                st.insert(i);
            }
            else{
                ans[i] = -1;
                if(mp.count(rains[i])){
                    auto it = st.lower_bound(mp[rains[i]]);
                    if(it == st.end()){
                        return {};
                    }
                    ans[*it] = rains[i];
                    st.erase(it);
                }
                mp[rains[i]] = i;
            }
        }
        return ans;
    }
};

10.14

Painting the Walls

数据范围：

我的思路：

整体数据范围较小，可以考虑用深度优先搜索的方法进行计算。

class Solution {
public:
    int memo(vector<int>& cost , vector<int> &time , int index , int walls , vector<vector<int>> &dp){
        if(walls <= 0){
            return 0;
        }
        if(index < 0){
            return 1e9;
        }
        if(dp[index][walls] != -1){
            return dp[index][walls];
        }
        int notTake = 0 + memo(cost , time , index-1 , walls , dp);
        int take = cost[index] + memo(cost , time , index-1 , walls-time[index]-1 , dp);
        return dp[index][walls] = min(notTake , take);
    }
    int paintWalls(vector<int>& cost, vector<int>& time) {
        int n = cost.size();
        vector<vector<int>> dp(n+1 , vector<int>(n+1 , -1));
        return memo(cost , time , n-1 , n , dp);
    }
};

10.16

只出现一次的数字 III

数据范围：

我的思路：

这里使用位运算会方便一些，首先根据异或操作的性质，对所有元素进行异或操作之后会得到最终的a^b的值，根据这个值我们通过相反数按位与操作获得最后一位1

的位置信息，代表a和b在这一位上产生了异或，然后将整体数据分成两个大类，即：

• 在该位置上均为1；
• 在该位置上均为0；

因此再次进行遍历，将不同类别分别进行异或，得到最终的答案，代码如下：

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        int sum = 0;
        for(int num : nums){
            sum ^= num;
        }
        int tmp = (sum == INT_MIN ? sum : (sum & (-sum)));
        int a = 0 , b = 0;
        for(int num : nums){
            if(num&tmp){
                a ^= num;
            }
            else{
                b ^= num;
            }
        }
        return {a , b};
    }
};

10.17

Validate Binary Tree Nodes

数据范围：

我的思路：

先找到根节点，找到之后bfs搜索判断是否所有点处于同一个分支上，且是否有环。

class Solution {
public:
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
        vector<int> flag(n);
        fill(flag.begin() , flag.end() , false);
        //先找根节点
        for(int i = 0 ; i < n ; ++i){
            if(leftChild[i] != -1){
                flag[leftChild[i]] = true;
            }
            if(rightChild[i] != -1){
                flag[rightChild[i]] = true;
            }
        }
        int root = -1;
        for(int i = 0 ; i < n ; ++i){
            if(!flag[i]){
                root = i;
                break;
            }
        }
        if(root == -1){
            return false;
        }
        //cout<<root<<endl;
        fill(flag.begin() , flag.end() , false);
        queue<int> q;
        q.push(root);
        flag[root] = true;
        while(!q.empty()){
            int nn = q.size();
            while(nn--){
                root = q.front();
                q.pop();
                int left = leftChild[root];
                int right = rightChild[root];
                if((left != -1 && flag[left]) || (right != -1 && flag[right])){
                    return false;
                }
                if(left != -1 && !flag[left]){
                    q.push(left);
                    flag[left] = true;
                }
                if(right != -1 && !flag[right]){
                    q.push(right);
                    flag[right] = true;
                }
            }
        }
        for(int i = 0 ; i < n ; ++i){
            if(!flag[i]){
                cout<<i<<endl;
                return false;
            }
        }
        return true;
    }
};

最后发现可以用并查集做，只是需要构建一个状态数组保存之前访问过的点，代码如下：

class Solution {
    public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
        UnionFind uf = new UnionFind(n);
        for(int i = 0 ; i < n ; ++i){
            if(leftChild[i] >= 0 && !uf.union(i,leftChild[i])){
                return false;
            }
            if(rightChild[i] >= 0 && !uf.union(i , rightChild[i])){
                return false;
            }
        }
        return uf.components() == 1;
    }
}
class UnionFind{
    private final int n;
    private final int[] roots;
    private int components;

    UnionFind(int n){
        this.n = n;
        roots = new int[n];
        for(int i = 0 ; i < n ; ++i){
            roots[i] = i;
        }
        components = n;
    }

    public boolean union(int parent , int child){
        int rootParent = findRoot(parent);
        int rootChild = findRoot(child);

        if(rootParent == rootChild || rootChild != child){
            return false;
        }

        roots[rootChild] = rootParent;
        components--;
        return true;
    }

    private int findRoot(int v){
        while(v != roots[v]){
            roots[v] = roots[roots[v]];
            v = roots[v];
        }
        return v;
    }

    public int components(){
        return components;
    }
}

10.21

Constrained Subsequence Sum

数据范围：

我的思路：

这道题的基本思路还是动态规划，但是问题是如何控制在限定的步长中进行元素的删减。这里给出了基本的代码：

class Solution {
public:
    int constrainedSubsetSum(vector<int>& nums, int k) {
        int n = nums.size();
        deque<int> q;//队尾保存当前的最大值
        int res = nums[0];
        for(int i = 0 ; i < n ; ++i){
            nums[i] += q.size() ? q.front() : 0;
            res = max(res , nums[i]);
            while(q.size() && nums[i] > q.back()){
                q.pop_back();
            }
            if(nums[i] > 0){
                q.push_back(nums[i]);
            }
            if(i >= k && q.size() && q.front() == nums[i-k]){
                q.pop_front();
            }
        }
        return res;
    }
};

• 将当前元素 nums[i] 与队列 q 的前端元素相加，这是因为在计算子集和时，可以选择加入队列中的元素以增加子集的和。
• 更新 res，以确保它存储当前的最大和。
• 检查队列 q，如果当前元素 **nums[i]**大于队列中的尾部元素，就一直从队尾弹出元素，直到队列为空或者直到当前元素小于队尾元素。这是因为队列 q 保存了当前窗口范围内的最大值。
• 如果当前元素 nums[i] 大于0，将其添加到队列 q，因为它有可能对后续子集的和有正面影响。
• 检查是否已经达到约束大小 k，如果是，则检查队列 q 的前端元素是否与在窗口范围内的最早元素 nums[i-k] 相等，如果相等，说明该元素已经不在窗口范围内了，因此从队列的前端弹出。

10.22

Maximum Score of a Good Subarray

数据范围：

我的思路：

首先这里给出了中心点，即最后的答案都是围绕k点进行计算的，因此可以使用双指针对两侧进行遍历，得到最大值。

class Solution {
public:
    int maximumScore(vector<int>& nums, int k) {
        int res = nums[k];
        int mini = nums[k];
        int i=k,j=k,n=nums.size();
        while(i > 0 || j < n-1){
            if(i == 0){
                ++j;
            }
            else if(j == n-1){
                --i;
            }
            else if(nums[i-1] < nums[j+1]){
                ++j;
            }
            else{
                --i;
            }
            mini = min(mini , min(nums[i] , nums[j]));
            res = max(res , mini * (j-i+1));
        }
        return res;
    }
};

10.23

Power of Four

数据范围：

我的思路：

这里给出了位运算的做法，首先分析是否整数，然后是以下两条定理的应用：

• 对于正整数n，和n-1的与运算结果为0，证明n为偶数；
• 对于正整数n，和0x55555555进行与运算如果结果为本身，则证明n的因子只有4、它本身和1。

代码如下：

class Solution {
public:
    bool isPowerOfFour(int n) {
        int mask = 0x55555555;
        return n > 0 && (n&(n-1))==0 && (n&mask)==n;
    }
};

10.25

K-th Symbol in Grammar

数据范围：

我的思路：

数据范围不算很大，这里直接构建一个栈来保存所求k节点上一轮的生成节点，因为每一组字符串的起点都是01开始，因此只要确认最开始是从0还是1开始的，就可以根据所在词组的奇偶位置来判断0还是1.具体的代码如下所示：

class Solution {
public:
    int kthGrammar(int n, int k) {
        stack<int> s;
        --k;
        s.push(k);
        while(k>1){
            k /= 2;
            s.push(k);
        }
        int start = s.top() == 0 ? 0 : 1;
        s.pop();
        int check[2][2] = {{1,0},{0,1}};
        int index;
        while(!s.empty()){
            int tmp = s.top();
            s.pop();
            if(start){
                index = 0;
            }
            else{
                index = 1;
            }
            start = tmp%2 ? check[index][1] : check[index][0];
        }
        return start;
    }
};

10.29

Poor Pigs

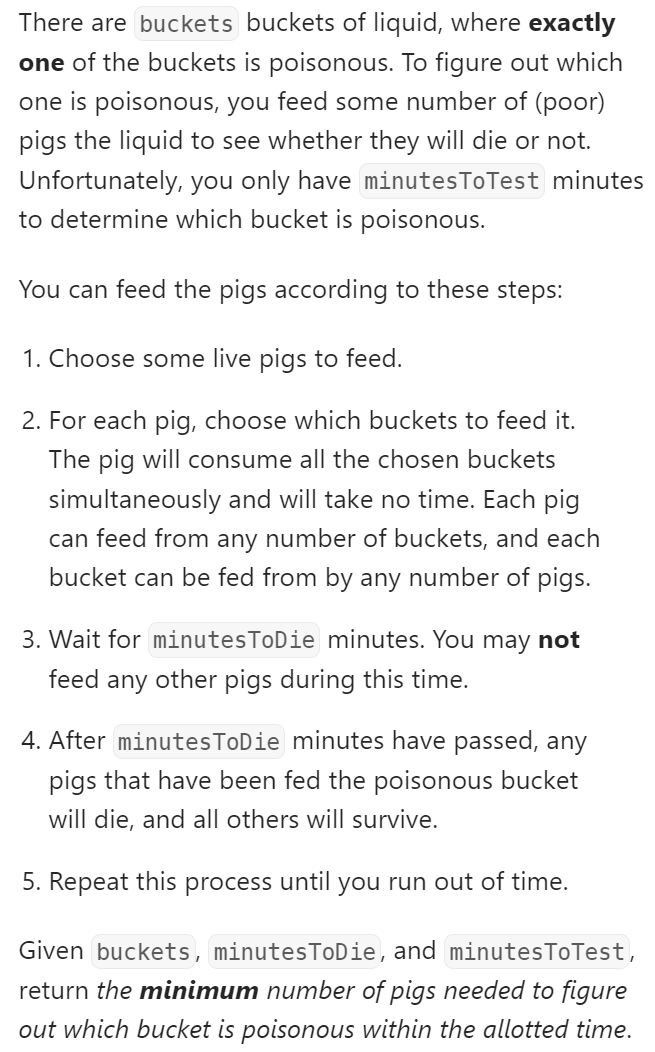
数据范围：

我的思路：

这道题很有意思，之前以为是二分，结果发现公式构造不出来，如果简单地将猪的数量进行左右收敛其实很难得到结果，对于不同的例子可能会得到相反的答案。看了答案之后才明白，这里对猪进行T轮测试，实际上会得到T+1轮结果。在每次进行均分样本测试时，我们可以单独抽出一组不做投喂，如果没有猪病死，证明问题出现在未实验的群组里。

class Solution {
public:
    int poorPigs(int buckets, int timeDetect, int timeTest) {
        return ceil(log2(buckets)/log2(int(timeTest/timeDetect)+1));
    }
};

10.30

Sort Integers by The Number of 1 Bits

数据范围：

我的思路：

感觉做法有些麻烦，就是构造字节数量数组进行排序。

class Solution {
public:
    int mp[10001];
    bool compare(int a , int b){
        if(mp[a] != mp[b]){
            return mp[a] > mp[b];
        }
        return a >= b;
    }
    vector<int> sortByBits(vector<int>& arr) {
        int n = arr.size();
        fill(mp,mp+10001,0);
        for(int nums : arr){
            if(mp[nums]!=0){
                continue;
            }
            int num = nums;
            while(num){
                if(num&1){
                    ++mp[nums];
                }
                num = num >> 1;
            }
        }
        for(int i = 0 ; i < n ; ++i){
            for(int j = i+1 ; j < n ; ++j){
                if(compare(arr[i],arr[j])){
                    int tmp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = tmp;
                }
            }
        }
        return arr;
    }
};

结果打开题解一看，发现stl里面有固定函数，直接套了一下。

class Solution {
public:
    vector<int> sortByBits(vector<int>& arr) {
        sort(arr.begin(), arr.end(), [](int a, int b) {
            int countA = __builtin_popcount(a);
            int countB = __builtin_popcount(b);
            return (countA == countB) ? a < b : countA < countB;
        });
        return arr;
    }
};

https://blog.csdn.net/github_38148039/article/details/109598368

函数功能就是返回输入数据中的二进制1的个数，说实话这个实现看起来比较规范，但是没看懂是咋实现的。

unsigned popcount (unsigned u)
{
    u = (u & 0x55555555) + ((u >> 1) & 0x55555555);
    u = (u & 0x33333333) + ((u >> 2) & 0x33333333);
    u = (u & 0x0F0F0F0F) + ((u >> 4) & 0x0F0F0F0F);
    u = (u & 0x00FF00FF) + ((u >> 8) & 0x00FF00FF);
    u = (u & 0x0000FFFF) + ((u >> 16) & 0x0000FFFF);
    return u;
}

10.31

每棵子树内缺失的最小基因值

数据范围：

我的思路：

数据范围不是很大，感觉正常思路深度搜索就能处理，整体上应该是自底向上的递归过程，对于每个节点构成的子树，基因集合构造完成后找寻缺失值即可。

$$\left.geneSet_{node}=\left\{\begin{matrix}nums[node]\end{matrix}\right.\right\}\bigcup\left(\sum_{chuld\in children_{node}}geneSet_{child}\right)$$

class Solution {
public:
    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
        int n = parents.size();
        vector<vector<int>> grid(n);
        for(int i = 1 ; i < n ; ++i){
            grid[parents[i]].push_back(i);
        }        
        vector<int> res(n,1);
        vector<unordered_set<int>> geneSet(n);
        function<int(int)> dfs = [&](int node) -> int {
            geneSet[node].insert(nums[node]);
            for(auto child : grid[node]){
                res[node] = max(res[node] , dfs(child));
                if(geneSet[node].size() < geneSet[child].size()){
                    geneSet[node].swap(geneSet[child]);
                }
                geneSet[node].merge(geneSet[child]);
            }
            while(geneSet[node].count(res[node]) > 0){
                res[node]++;
            }
            return res[node];
        };
        dfs(0);
        return res;
    }
};